Definición: Las rectas paralelas son aquellas que tienen la misma pendiente y se encuentran incluidas dentro de un mismo plano, pero que no poseen puntos en común, es decir, no existe un punto de intersección entre ellas.
Rectas paralelas en el plano cartesiano
Dos rectas en el plano cartesiano son paralelas si tienen la misma pendiente \(m\) e interceptan al eje vertical \(y\) en puntos diferentes \(b\) y \(c\). La siguiente imagen muestra dos rectas paralelas en el plano cartesiano.
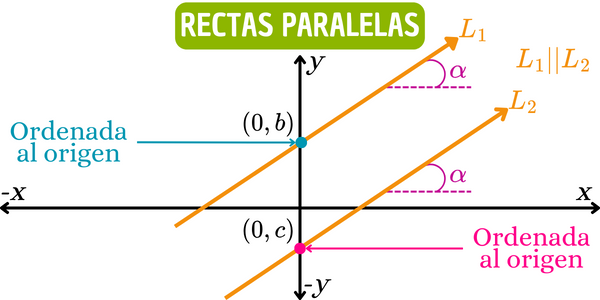
¿Cómo saber si dos rectas son paralelas?
Dos rectas son paralelas si tienen pendientes iguales e interceptan al eje vertical en puntos diferentes. Matemáticamente, si \(m_1\) es la pendiente de la recta \(L_1\) e intercepta al eje vertical en \(y=b\) y \(m_2\) es la pendiente de la recta \(L_2\) que intercepta al eje vertical en \(y=c\), entonces la recta \(L_1\) es paralela a la recta \(L_2\) si: \[m_1=m_2\] y \[b\neq c\]
Ejemplo 1. Determina si la recta \(L_1\) que pasa por los puntos (-3, -1) y (2, 4) es paralela a la recta \(L_2\) que pasa por los puntos (2, -6) y (7, -1).
Solución: Para determinar si dos rectas son paralelas se debe conocer la pendiente y la ordenada al origen de cada recta (punto de intersección de la recta con el eje vertical \(y\)). De tal manera que, si las pendientes de las rectas son iguales y el valor de las ordenadas al origen es diferente, es decir, interceptan al eje \(y\) en distintos puntos, entonces las rectas son paralelas.
Dado que se conocen las coordenadas de los puntos por los que pasan las rectas, se puede determinar el valor de la pendiente de cada recta a través de estos puntos. La fórmula para calcular la pendiente de la recta que pasa por dos puntos \(P_1\) y \(P_2\) de coordenadas \((x_1, y_1)\) y \((x_2, y_2)\) respectivamente, es: \[m=\frac{y_2-y_1}{x_2-x_1}\]
Aplicando esta fórmula, obtenemos que la pendiente de la recta que pasa por los puntos (-3, -1) y (2, 4) es: \[\begin{aligned}m&=\frac{y_2-y_1}{x_2-x_1}\\&=\frac{4-(-1)}{2-(-3)}\\&=\frac{4+1}{2+3}\\&=\frac{5}{5}\\&=1\end{aligned}\]
Para hallar la ordenada al origen de la recta que pasa por los puntos (-3, -1) y (2, 4), se sustituye el valor de la pendiente de la recta y las coordenadas de alguno de los puntos en la ecuación \(y=mx+b\) y se resuelve para \(b\). Al sustituir las coordenadas (2, 4), obtenemos que la ordenada al origen es: \[\begin{aligned}y&=mx+b\\4&=1\cdot 2+b\\4&=2+b\\4-2&=b\\2&=b\end{aligned}\]
Por otra parte, la pendiente de la recta que pasa por los puntos (2, -6) y (7, -1) es: \[\begin{aligned}m&=\frac{y_2-y_1}{x_2-x_1}\\&=\frac{-1-(-6)}{7-2}\\&=\frac{-1+6}{5}\\&=\frac{5}{5}\\&=1\end{aligned}\]
Para obtener la ordenada al origen de la recta que pasa por los puntos (2, -6) y (7, -1), se sustituye el valor de la pendiente de la recta \(m=1\) y las coordenadas de alguno de los puntos en la ecuación \(y=mx+b\) y se resuelve para \(b\). Al sustituir las coordenadas (7, -1), obtenemos que la ordenada al origen es: \[\begin{aligned}y&=mx+b\\-1&=1\cdot 7+b\\-1&=7+b\\-1-7&=b\\-8&=b\end{aligned}\]
Como las pendientes de ambas rectas son iguales a 1 e interceptan al eje vertical en puntos diferentes, 2 y -8, entonces las rectas son paralelas.
Ecuación de la recta paralela a otra que pasa por un punto
Para encontrar la ecuación de una recta paralela a otra, es necesario conocer, además de su pendiente, un punto por el cual pasa dicha recta.
En términos más formales, para hallar la ecuación de una recta \(L_2\) que sea paralela a una recta \(L_1\), es necesario conocer las coordenadas \((x_1, y_1)\) de un punto \(P_1\) por el cual pase la recta \(L_2\). Además, si \(L_2\) es paralela a \(L_1\), entonces sus pendientes son iguales, es decir: \[m_2=m_1\]
Por lo tanto, al conocer las coordenadas de un punto por el que pasa la recta y la pendiente de ésta, se puede determinar su ecuación en la forma punto-pendiente: \[y-y_1=m(x-x_1)\], donde \((x_1, y_1)\) son las coordenadas de un punto por el cual pasa la recta, y \(m\) es la pendiente de la recta.
A continuación, veamos algunos ejemplos para clarificar este proceso.
Ecuación de la recta paralela que pasa por un punto
Ejemplo 2. Calcula la ecuación de una recta paralela a la recta \(y=x-5\) y que pase por el punto (-2, 1).
Solución: El primer paso para hallar la ecuación de una recta paralela a otra consiste en identificar el valor de la pendiente de la recta conocida. La pendiente de una recta es el coeficiente de la variable \(x\) en la ecuación \(y=mx+b\). Así, la pendiente de la recta definida por la ecuación \(y=x-5\) es \(m=1\).
El segundo paso consiste en asignarle el mismo valor de la pendiente de la recta conocida a la pendiente de la recta paralela, ya que las rectas paralelas tienen pendientes iguales. Por lo tanto, la pendiente de la recta paralela será \(m_2=1\).
Ahora que se conoce la pendiente de la recta paralela y además se conoce un punto por el que esta pasa, se puede hallar su ecuación en la forma punto-pendiente: \[y-y_1=m(x-x_1)\]
El tercer paso consiste en sustituir las coordenadas del punto dado (-2, 1) y la pendiente \(m_2=1\) en la forma punto-pendiente: \[\begin{aligned}y-1&=1(x-(-2))\\y-1&=(x+2)\end{aligned}\]
Por lo tanto, la ecuación de la recta paralela a \(y=x-5\) y que pasa por el punto (-2, 1) en la forma punto-pendiente es: \[y-1=x+2\]
Para obtener la ecuación en la forma pendiente-ordenada al origen, despejamos \(y\): \[\begin{aligned}y-1&=x+2\\y&=x+2+1\\&=x+3\end{aligned}\]
Así, la ecuación de la recta paralela a \(y=x-5\) y que pasa por el punto (-2, 1) en la forma pendiente-ordenada al origen es: \[y=x+3\]
Ejemplo 3. Encuentra la ecuación de la recta paralela a \(x+2y+3=0\) que pasa por el punto (3, 5).
Solución. El primer paso para hallar la ecuación de una recta paralela a otra consiste en identificar el valor de la pendiente de la recta conocida. Observa que en este caso la ecuación de la recta está en la forma general.
La ecuación general de la recta (ecuación implícita) se expresa como: \[Ax+By+C=0\], donde \(A\) y \(B\) son coeficientes constantes, con \(B \neq 0\) y donde \(C\) es el término constante (término independiente) de la ecuación. Dado que la ecuación general de la recta representa una recta en el plano cartesiano, tanto el valor de la pendiente \(m\) como el punto de intersección \(b\) de la recta con el eje vertical \(y\) (ordenada al origen) se obtienen al expresar a \(y\) como una función de \(x\), es decir, se obtienen al despejar \(y\) de la ecuación general.
Al despejar \(y\), obtenemos: \[y=-\frac{A}{B}x-\frac{C}{B}\] que proporciona la ecuación explícita \(y=mx+b\), donde \(m\) es la pendiente de la recta y \(b\) es la ordenada al origen, es decir: \[\begin{aligned}m&=-\frac{A}{B}\\b&=-\frac{C}{B}\end{aligned}\]
A la ecuación explícita \(y=mx+b\) también se le conoce como ecuación ordinaria de la recta, ecuación pendiente-intersección o más comúnmente ecuación de la recta en la forma pendiente-ordenada al origen.
Entonces, para identificar el valor de la pendiente de la recta a partir de la ecuación general \(x+2y+3=0\), simplemente debemos despejar \(y\):
De esta manera, obtenemos que la pendiente de la recta definida por la ecuación \(x+2y+3=0\) es \(m=-\frac{1}{2}\).
El segundo paso consiste en asignarle el mismo valor de la pendiente de la recta conocida a la pendiente de la recta paralela, ya que las rectas paralelas tienen pendientes iguales. Por lo tanto, la pendiente de la recta paralela será \(m_2=-\frac{1}{2}\).
Ahora que conocemos la pendiente de la recta paralela y además conocemos un punto por el que esta pasa, podemos hallar su ecuación en la forma punto-pendiente. Para esto, simplemente debemos sustituir las coordenadas del punto (3, 5) y la pendiente \(m_2=-\frac{1}{2}\) en la forma punto-pendiente: \[y-y_1=m(x-x_1)\]
Sustituyendo, obtenemos: \[\begin{aligned}y-5&=-\frac{1}{2}(x-3)\end{aligned}\]
Por lo tanto, la ecuación de la recta paralela \(x+2y+3=0\) que pasa por el punto (3, 5) en la forma punto-pendiente es: \[y-5=-\frac{1}{2}(x-3)\]
Para expresar la ecuación de una recta que se encuentra en la forma punto-pendiente en la forma general, debemos multiplicar ambos miembros de la ecuación punto-pendiente por el denominador del valor de la pendiente (si la pendiente es una fracción), igualar a cero la ecuación y simplificar la ecuación si es necesario.
El procedimiento para convertir la ecuación punto-pendiente \( y-5=-\frac{1}{2}(x-3)\) a la forma general se muestra a continuación:
De esta manera, obtenemos que la ecuación de la recta paralela a \(x+2y+3=0\) que pasa por el punto (3, 5) en la forma general es: \[x+2y-13=0\]
Ejemplo 4. ¿Cuál debe ser el valor del coeficiente \(k\) para que las rectas \(x+2y-3=0\) y \(x-ky+4=0\) sean paralelas?
Solución: La condición que debe cumplirse para que dos rectas sean paralelas es que el valor de sus pendientes sea el mismo y que además intercepten al eje vertical \(y\) en puntos diferentes. Por lo tanto, las rectas \(x+2y-3=0\) y \(x-ky+4=0\) son paralelas si el valor de sus pendientes es el mismo.
Observa que las ecuaciones de las rectas están en la forma general (forma implícita), es decir, están en la forma: \[Ax+By+C=0\]
La pendiente de la recta a partir de la ecuación general de la recta está definida como: \[m=-\frac{A}{B}\]
Entonces, la pendiente de la recta \(x+2y-3=0\) es: \[m_1=-\frac{1}{2}\] y la pendiente de la recta \(x-ky+4=0\) es: \[\begin{aligned}m_2&=-\frac{1}{-k}\\&=\frac{1}{k}\end{aligned}\]
Entonces, para que las rectas sean paralelas debe cumplirse que el valor de sus pendientes sea igual, es decir, debe cumplirse que: \[-\frac{1}{2}=\frac{1}{k}\]
De esta igualdad despejamos \(k\) para hallar el valor del coeficiente que hace que las rectas sean paralelas: \[\begin{aligned}-\frac{1}{2}&=\frac{1}{k}\\2&=k\end{aligned}\]
Por lo tanto, el valor del coeficiente \(k\) que hace que las rectas \(x+2y-3=0\) y \(x-ky+4=0\) sean paralelas es \(k=2\), es decir, las rectas son paralelas si éstas son \(x+2y-3=0\) y \(x-2y+4=0\).
A continuación, veamos una manera distinta de hallar la ecuación de una recta paralela a otra a partir de su ecuación en la forma general.
Teorema 5. Sea \(Ax+By+C=0\) la ecuación general de una recta \(L_1\) y \(Ax+By+D=0\) la ecuación general de una recta \(L_2\). Las rectas \(L_1\) y \(L_2\) son paralelas si sus ecuaciones difieren en el término constante, es decir, si \(C\neq D\).
Demostración: De acuerdo con la definición de rectas paralelas, dos rectas son paralelas si tienen la misma pendiente e interceptan al eje vertical \(y\) en diferentes puntos.
Entonces, si \(Ax+By+C=0\) es la ecuación general de una recta \(L_1\), al despejar \(y\) de esta ecuación obtenemos:
En esta ecuación, \(-\frac{A}{B}\) corresponde a la pendiente de la recta y \(-\frac{C}{B}\) corresponde a la ordenada al origen, es decir, al punto donde la recta intercepta al eje vertical \(y\).
Ahora bien, si \(Ax+By+D=0\) es la ecuación general de una recta \(L_2\), al despejar \(y\) de esta ecuación obtenemos:
En esta ecuación, \(-\frac{A}{B}\) corresponde a la pendiente de la recta y \(-\frac{D}{B}\) corresponde a la ordenada al origen, es decir, al punto donde la recta intercepta al eje vertical \(y\).
Como puedes observar, ambas ecuaciones tienen la misma pendiente \(-\frac{A}{B}\); sin embargo, interceptan al eje vertical \(y\) en diferentes puntos: la recta \(L_1\) en \(b=-\frac{C}{B}\) y la recta \(L_2\) en \(b=-\frac{D}{B}\). Por lo tanto, como la pendiente es la misma pero el punto de intersección es diferente, entonces las rectas son paralelas. Es decir, dos rectas son paralelas si sus respectivas ecuaciones en la forma general difieren únicamente en el término independiente (término constante).
Ejemplo 6. Determina la ecuación de una recta paralela a otra cuya ecuación es \(3x+2y+5=0\).
Solución: De acuerdo con el teorema 1, dos rectas son paralelas si sus ecuaciones en la forma general difieren solo en el valor del término constante (término independiente). Por lo tanto, la ecuación de una recta paralela a la recta \(3x+2y+5=0\) puede ser simplemente \(3x+2y+7=0\). Esto se debe a que estas ecuaciones se encuentran en la forma general y difieren únicamente en el término independiente. El término independiente de una es 5 y el de la otra es 7. Por lo tanto, las rectas definidas por las ecuaciones \(3x+2y+5=0\) y \(3x+2y+7=0\) son paralelas.
Ejemplo 7. Encuentra la ecuación de la recta paralela a \(3x+2y-4=0\) que pasa por el punto (2, 3).
Solución: De acuerdo con el teorema 1, dos rectas son paralelas si sus ecuaciones en la forma general difieren únicamente en el valor del término constante (término independiente). Por lo tanto, la ecuación de una recta paralela a la recta \(3x+2y-4=0\) puede ser simplemente \(3x+2y+k=0\), donde \(k \neq -4\).
Para hallar el valor del término constante \(k\), simplemente se deben sustituir las coordenadas del punto (2, 3) en la ecuación \(3x+2y+k=0\) y resolver para \(k\). Sustituyendo las coordenadas del punto y despejando \(k\), obtenemos:
Por lo tanto, la ecuación de una recta paralela a \(3x+2y-4=0\) que pasa por el punto (2, 3) es: \[3x+2y-12=0\]
Rectas paralelas a los ejes de coordenadas
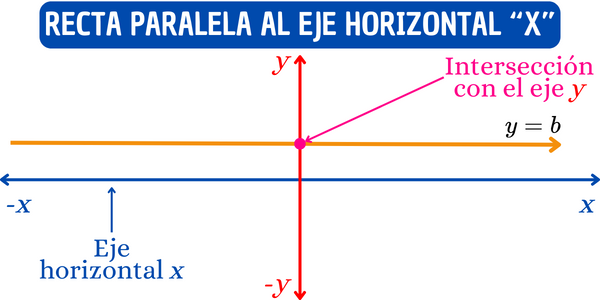
Recta paralela al eje x
Una recta paralela al eje x es una línea horizontal. La ecuación de una recta horizontal es \[y=b\], donde \(b\) es la ordenada al origen, es decir, el punto donde la recta corta el eje vertical \(y\). Una recta horizontal es aquella cuyo valor de la pendiente es igual a cero, lo que significa que la línea no tiene inclinación en dirección vertical \(y\). Por ejemplo, la recta definida por la ecuación \(y=3\) es paralela al eje horizontal \(x\) e intercepta al eje \(y\) en \(x=3\).
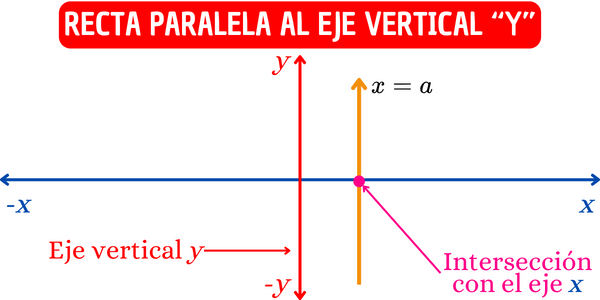
Recta paralela al eje y
Una recta paralela al eje \(y\) es una recta vertical. La ecuación de una recta vertical está definida como: \[x=a\], donde \(a\) es el punto donde la recta corta el eje \(x\). Una recta vertical es aquella cuyo valor de la pendiente no está definido, lo que significa que la recta no tiene inclinación en dirección horizontal \(x\). Por ejemplo, la línea definida por la ecuación \(x=-2\) es paralela al eje vertical \(y\) e intercepta al eje \(x\) en \(x=-2\).