El Plano Cartesiano
El plano cartesiano, también conocido como sistema de coordenadas cartesianas, debe su nombre al ilustre matemático y filósofo francés René Descartes, quien lo desarrolló en el siglo XVII. Su invención revolucionó el campo de las matemáticas al proporcionar una forma precisa de relacionar los números y la geometría. Gracias al plano cartesiano, fue posible establecer una conexión profunda entre el álgebra y la geometría, sentando las bases para el nacimiento del análisis matemático moderno.

Componentes del plano cartesiano
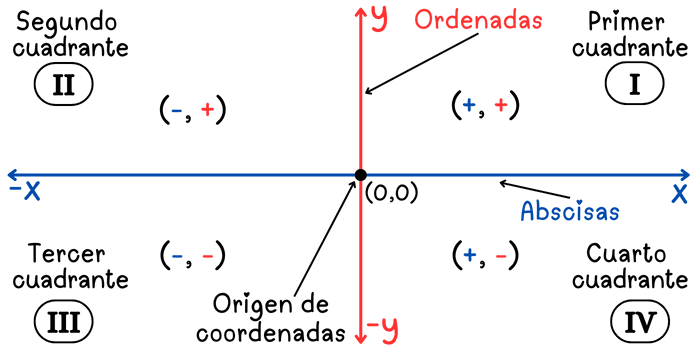
El plano cartesiano está compuesto por dos componentes esenciales: El eje \(x\) y el eje \(y\). Estos ejes se intersectan en el origen de coordenadas \((0, 0)\) y se extienden infinitamente en direcciones positivas y negativas.
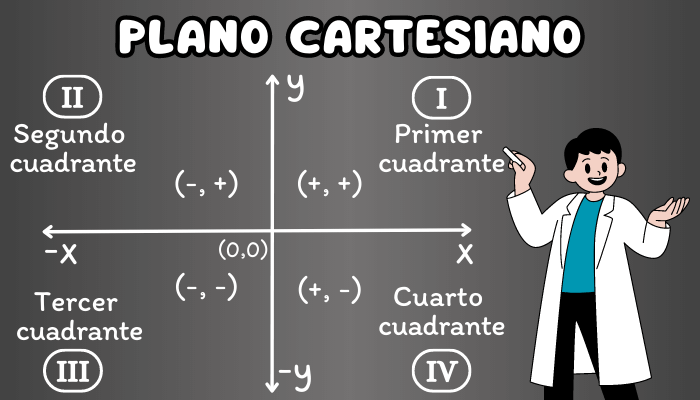
El eje \(x\) representa la coordenada horizontal, también conocida como abscisa, mientras que el eje \(y\) representa la coordenada vertical, también conocida como ordenada. El plano cartesiano está dividido en 4 partes iguales, a cada una de estas partes se le denomina cuadrante. Los cuadrantes se enumeran con los números romanos: I, II, III y IV, y en sentido contrario al giro de las manecillas del reloj. En cada uno de los cuadrantes se cumple lo siguiente: Primer cuadrante: Abscisas positivas y ordenadas positivas. Segundo cuadrante: Abscisas negativas y ordenadas positivas. Tercer cuadrante: Abscisas negativas y ordenadas negativas. Cuarto cuadrante: Abdicas positivas y ordenadas negativas.
¿Cómo se hace un plano cartesiano?
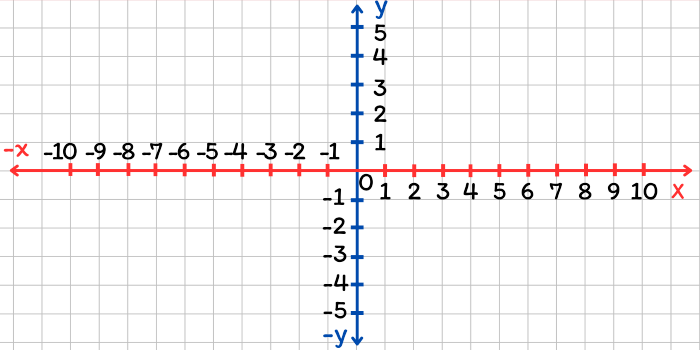
Para comenzar, necesitarás algunos materiales básicos, como un papel cuadriculado o papel milimétrico, un lápiz y una regla. El primer paso consiste en dibujar los ejes. Inicia con una hoja de papel en posición horizontal. Dibuja una línea horizontal en la parte media del papel, que servirá como el eje de las abscisas \(x\). Luego, traza una línea vertical en la parte media del papel, que representará el eje de las ordenadas \(y\). El punto donde estas dos líneas se cruzan es el punto de origen de coordenadas, que se representa simplemente como \(0\) o como \((0, 0)\). A continuación, marca las divisiones en los ejes. Divide los ejes horizontal \(x\) y vertical \(y\) en segmentos iguales y numéricamente consistentes. Estos segmentos se utilizan para medir distancias en el plano cartesiano, por lo que es esencial que tengan la misma distancia en ambos ejes para mantener una escala adecuada. Finalmente, etiqueta los ejes con los números correspondientes. A lo largo del eje \(x\), a la izquierda del origen, coloca los números negativos, y a la derecha del origen, coloca los valores positivos. En cuanto al eje \(y\), ubica los números positivos arriba del origen y los números negativos abajo del origen. Esta disposición permite representar números positivos y negativos en ambas direcciones. La siguiente imagen muestra como debe quedar el plano cartesiano.
Crear un plano cartesiano es esencial para realizar gráficos, resolver ecuaciones y visualizar datos en matemáticas. Siguiendo estos pasos, podrás establecer un sistema de coordenadas claro y preciso que te ayudará a representar relaciones y datos de manera efectiva.
Plano cartesiano: coordenadas y puntos
Una de las maravillas del plano cartesiano radica en su capacidad para representar puntos en el espacio bidimensional mediante coordenadas. Cada punto \(P\) en el plano se describe mediante un par ordenado \((x, y)\), donde \(x\) representa la coordenada horizontal y \(y\) representa la coordenada vertical. Al identificar las coordenadas de un punto en el plano cartesiano, podemos determinar su ubicación exacta y explorar relaciones entre diferentes puntos. En general, un punto \(P\) en el plano cartesiano de escribe como: \(P(x, y)\)
Plano cartesiano ejemplos
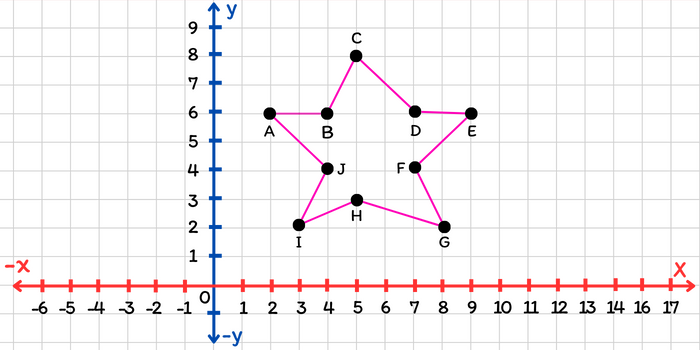
Ejemplo 1. Ubicar los siguientes puntos en el plano cartesiano: \[\begin{aligned}&A(2, 6), B(4, 6), C(5, 8)\\&D(7, 6), E(9, 6), F(7, 4)\\&G(8, 2), H(5, 3), I(3, 2)\end{aligned}\] Observa que, el punto \(A\) tiene coordenadas \((2, 6)\), es decir, su coordenada horizontal es 2 y su coordenada vertical es 6. Para ubicar este punto en el plano, buscamos y señalamos en el eje \(x\) el número 2 y a partir de ahí buscamos y señalamos en el eje \(y\) el número 6. El lugar al que se llega corresponde a la ubicación de punto \(A\). La siguiente imagen muestra la ubicación en el plano cartesiano de cada uno de los puntos del enunciado.
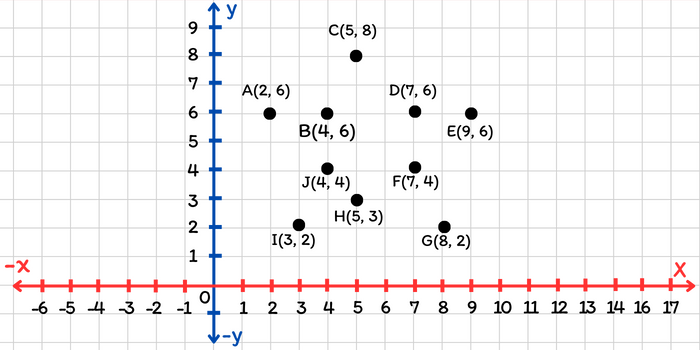
Puede ser que a simple vista la ubicación de cada punto carezca de sentido, sin embargo, podemos relacionar estos puntos de alguna manera para formar alguna figura. Por ejemplo, si unimos los puntos siguiendo el orden del abecedario obtenemos la siguiente figura:
Ejemplo 2. Escriba los pares ordenados de los puntos A, B, C y D ubicados en el plano cartesiano.
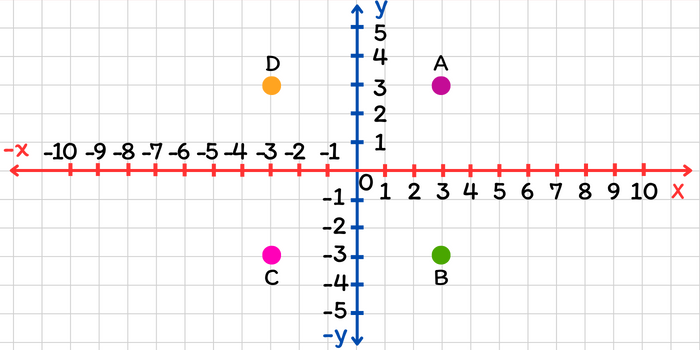
Solución: El objetivo de este ejemplo es identificar de manera correcta las coordenadas de cada uno de los puntos. Observa que la coordenada en \(x\) del punto A se encuentra en \(x=3\) y la coordenada \(y\) está en \(y=3\). La coordenada en \(x\) del punto B se encuentra en \(x=3\) y la coordenada en \(y\) se encuentra en \(y=-3\). La coordenada en \(x\) del punto C se encuentra en \(x=-3\) y su coordenada en \(y\) está en \(y=-3\). Para el punto D, la coordenada en \(x\) está en \(x=-3\) y la coordenada en \(y\) en \(y=3\). Por lo tanto, las coordenadas de los puntos son: \[\begin{aligned}A&(3, 3)\\B&(3, -3)\\C&(-3, -3)\\D&(-3, 3)\end{aligned}\]
Gráfica de una función en el plano cartesiano
El plano cartesiano también es fundamental para representar gráficamente funciones matemáticas. Mediante ecuaciones y funciones, podemos trazar gráficas en el plano cartesiano y visualizar cómo las diferentes formas de las ecuaciones se reflejan en las formas de las gráficas correspondientes. Desde las rectas lineales hasta las curvas complejas de las funciones cuadráticas, cúbicas u otras, el plano cartesiano nos permite explorar la relación entre variables y analizar sus comportamientos.
Ejemplo 3. Sea \(f\) una función de variable real definida como \(f(x)=x^2\), la gráfica de esta función es la representación de todos los pares ordenados \((x, f(x))\) de la función en el plano cartesiano. Si deseamos construir la gráfica de esta función, debemos construir una tabla de valores \((x, f(x))\). Aquí, los valores que toma \(x\), son aquellos que se encuentran en el dominio de la función \(f\) y los valores \(f(x)\) son aquellos que se obtienen de evaluar \(x\) en la función. Como el dominio de una función cuadrática es el conjunto de todos los números reales \(\mathbb{R}\), entonces podemos asignarle a \(x\) cualquier valor. En este caso le asignaremos únicamente los siguientes valores: \[\left\lbrace-2, -1, 0, 1, 2 \right\rbrace\] Evaluando cada uno de estos valores en la función, obtenemos la siguiente tabla.

Como cada fila de la tabla es de la forma \((x, f(x))\), podemos ubicar estas coordenadas en el plano cartesiano para obtener la los puntos que conforman la gráfica de la función. La siguiente imagen muestra la ubicación en el plano cartesiano de cada uno de los puntos de la tabla.
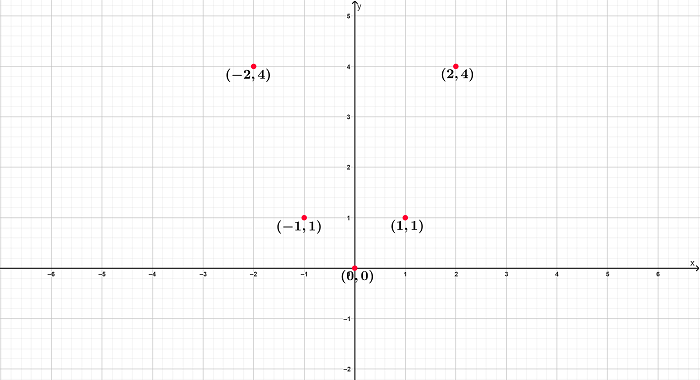
La idea de graficar una función mediante algunos de sus puntos consiste en unir dichos puntos para tener una aproximación visual de la gráfica real de la función. Como podrás imaginar, mientras más valores asignes a \(x\), más valores de \(f(x)\) tendrás y, por lo tanto, obtendrás más puntos para ubicar en el plano.
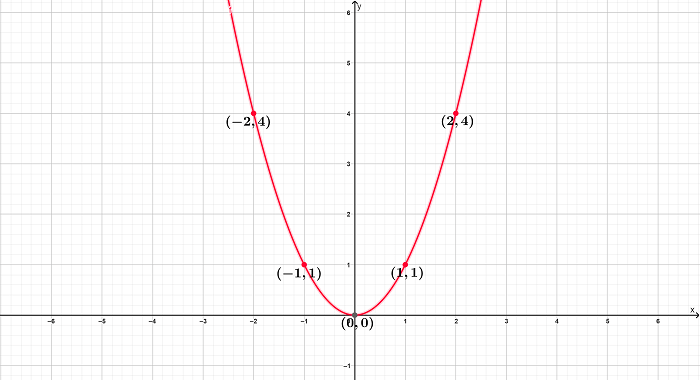
Plano cartesiano ejercicios para practicar
Ejercicio 1. Identificar coordenadas: Dado el siguiente conjunto de puntos en el plano cartesiano, identifica las coordenadas \((x, y)\) de cada punto: \[\begin{aligned}A&(2, 3)\\B&(-1, -4)\\C&(0, 0)\\D&(5, -2)\\E&(-3, 6)\end{aligned}\]
Ejercicio 2. Graficar puntos: Grafica los siguientes puntos en un plano cartesiano: \[\begin{aligned}F&(4, 2)\\G&(-2, 5)\\H&(0, -3)\\I&(3, 0)\\J&(-4, -1)\end{aligned}\]
Ejercicio 3. Hallar la distancia entre puntos: Calcula la distancia entre los siguientes pares de puntos en el plano cartesiano utilizando la fórmula de la distancia: \[\begin{aligned}A(3, 2)\rightarrow B(7, 5)\\C(-1, -1)\rightarrow D(4, 3)\end{aligned}\]
Ejercicio 4. Identificar cuadrantes: Para cada uno de los siguientes puntos, identifica en cuál de los cuatro cuadrantes del plano cartesiano se encuentran ubicados: \[\begin{aligned}K&(3, 2)\\L&(-2, -4)\\M&(0, 1)\\N&(-5, 3)\\O&(1, -1)\end{aligned}\]
Ejercicio 5. Reflexión en el eje \(x\): Dado un conjunto de puntos en el plano cartesiano, encuentra las coordenadas de los puntos resultantes después de reflejarlos en el eje \(x\) (es decir, cambiar el signo de la coordenada \(y\)). Los puntos son los siguientes: \[\begin{aligned}A&(2, 3)\\B&(-1, -4)\\C&(0, 0)\\D&(5, -2)\\E&(-3, 6)\end{aligned}\]
Ejercicio 6. Reflexión en el eje \(y\): Dado un conjunto de puntos en el plano cartesiano, encuentra las coordenadas de los puntos resultantes después de reflejarlos en el eje \(y\) (es decir, cambiar el signo de la coordenada \(x\)). Los puntos son: \[\begin{aligned}A&(2, 3)\\B&(-1, -4)\\C&(0, 0)\\D&(5, -2)\\E&(-3, 6)\end{aligned}\]
Aplicaciones del plano cartesiano
Más allá de su importancia en las matemáticas, el plano cartesiano tiene aplicaciones prácticas en diversos campos. En la física, se utiliza para modelar trayectorias y analizar fuerzas. En la economía, ayuda a visualizar datos y analizar tendencias. En la programación, es esencial para el desarrollo de gráficos y juegos. En la geometría, permite explorar las propiedades de figuras y calcular áreas y volúmenes. Estos son solo algunos ejemplos de cómo el plano cartesiano se convierte en una valiosa herramienta en el mundo real.
En resumen: El sistema cartesiano de René Descartes desempeñó un papel fundamental en el desarrollo de las matemáticas modernas al establecer un vínculo entre el Álgebra y la Geometría. Esta conexión condujo a la creación de la Geometría Analítica, una herramienta que nos permite representar gráficamente figuras geométricas y analizar sus propiedades para la formulación de expresiones matemáticas. En particular, la Geometría Analítica resulta especialmente útil para representar gráficamente aquellas relaciones que varían de manera directamente proporcional.
Preguntas frecuentes
¿Qué es un plano cartesiano? Un plano cartesiano es un sistema de coordenadas bidimensional que se utiliza para representar puntos en el espacio utilizando dos ejes perpendiculares: el eje horizontal (llamado eje \(x\)) y el eje vertical (llamado eje \(y\)). Cada punto en el plano está definido por un par ordenado \((x, y)\), donde el valor de \(x\) representa la coordenada horizontal y el valor de \(y\) representa la coordenada vertical.
¿Quién inventó el plano cartesiano? El plano cartesiano fue desarrollado por el matemático y filósofo francés René Descartes en el siglo XVII. La idea de utilizar coordenadas numéricas para representar puntos en un espacio bidimensional fue una innovación fundamental en la historia de las matemáticas.
¿Cuáles son los elementos del plano cartesiano? Los elementos clave del plano cartesiano son: Eje \(x\): La línea horizontal que representa las coordenadas horizontales. Eje \(y\): La línea vertical que representa las coordenadas verticales. Origen: El punto donde se cruzan los ejes \(x\) e \(y\), con coordenadas \((0, 0)\). Cuadrantes: El plano se divide en cuatro cuadrantes numerados en sentido contrario al giro de las manecillas del reloj.
¿Cuál es la fórmula para hallar la distancia entre dos puntos en el plano cartesiano? La fórmula para calcular la distancia entre dos puntos en el plano cartesiano, con coordenadas \(A(x_{1}, y_{1})\) y \(B(x_{2}, y_{2})\), es: \[d=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\]
¿Qué es la simetría en el plano cartesiano? La simetría en el plano cartesiano se refiere a la correspondencia entre puntos en el plano que son equidistantes respecto a un eje. Hay dos tipos principales de simetría: Simetría respecto al eje \(x\): Un punto y su reflejo tienen la misma coordenada \(x\) pero coordenadas \(y\) opuestas. Simetría respecto al eje \(y\): Un punto y su reflejo tienen la misma coordenada \(y\) pero coordenadas \(x\) opuestas.