Intersección de dos rectas
Dos rectas se intersecan si existe un punto en común entre ellas. Una condición necesaria para que dos rectas se intercepten en un punto es que estas se encuentren en un mismo plano y que las rectas sean no paralelas. A continuación, veamos más información acerca del punto de intersección de dos rectas.
Punto de intersección de dos rectas
El punto en el que se intersecan (se cortan) dos rectas se denomina punto de intersección de las rectas. La siguiente imagen muestra la intersección de dos rectas en el plano cartesiano. Las rectas \(L_1\) y \(L_2\) se interceptan en el punto \(P_0\) de coordenadas \((x_0, y_0)\).
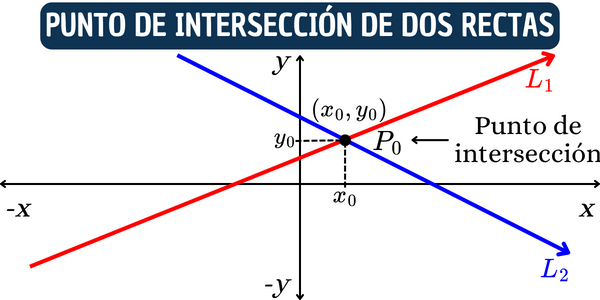
Si \(P_0\) es el punto de intersección de dos rectas \(L_1\) y \(L_2\), entonces tal punto pertenece a la recta \(L_1\) y también pertenece a la recta \(L_2\), es decir, las coordenadas \((x_0, y_0)\) del punto de intersección satisfacen las ecuaciones de las rectas \(L_1\) y \(L_2\). Gráficamente, el punto de intersección entre estas dos rectas es el punto donde las dos rectas son exactamente iguales.
¿Cómo hallar el punto de intersección de dos rectas?
Hallar el punto de intersección de dos rectas significa encontrar los valores de las coordenadas \((x_0, y_0)\) del punto de intersección \(P_0\) de las rectas. Esto implica hallar los valores de \((x_0)\) y \((y_0)\) que satisfacen ambas ecuaciones de las rectas simultáneamente. El procedimiento para calcular el punto de intersección de dos rectas varía según la forma en que estén expresadas las ecuaciones de las rectas.
Ecuación en la forma pendiente-ordenada al origen
Si las ecuaciones de las rectas \(L_1\) y \(L_2\) se encuentran en la forma pendiente-ordenada al origen: \[y=mx+b\] es decir, si la recta \(L_1\) está definida por la ecuación \[y=m_1x+b_1\] y la recta \(L_2\) está definida por la ecuación \[y=m_2x+b_2\] donde \(m_1\) y \(m_2\) corresponden a las pendientes de las recta, y \(b_1\) y \(b_2\) corresponden a las ordenadas al origen de las rectas, entonces el punto \(P_0\) de coordenadas \((x_0, y_0)\) es el punto de intersección de las rectas \(L_1\) y \(L_2\) si los valores de \(x_0\) y \(y_0\) satisfacen ambas ecuaciones de las rectas simultáneamente.
Los valores de las coordenadas \(x_0\) y \(y_0\) se obtienen al resolver el sistema de dos ecuaciones con dos incógnitas definido por las ecuaciones en la forma pendiente-ordenada al origen de las rectas.
Para encontrar los valores de las coordenadas \((x_0, y_0)\) del punto de intersección \(P\), primero se deben igualar las ecuaciones de las rectas para encontrar el valor de la coordenada \(x_0\) que satisface ambas ecuaciones. Luego, se resuelve para \(x_0\) y se sustituye el valor encontrado en alguna de las dos ecuaciones originales para hallar el valor correspondiente de la coordenada \(y_0\). Las coordenadas del punto de intersección \(P_0\) serán el par ordenado \((x_0, y_0) \) obtenido.
A continuación, veamos algunos ejemplos de cómo calcular el punto de intersección entre dos rectas a partir de sus ecuaciones en la forma pendiente-ordenada al origen.
Punto de intersección entre dos rectas ejemplos
Ejemplo 1. Calcula el punto de intersección entre las rectas \(L_1\) y \(L_2\) definidas por las ecuaciones: \[\begin{aligned}y&=3x-3\\y&=-x+1\end{aligned}\]
Solución. Calcular el punto de intersección de dos rectas consiste en hallar los valores de las coordenadas \(x_0\) y \(y_0\) del punto \(P(x_0, y_0)\) donde se interceptan las rectas.
El primer paso para hallar los valores de las coordenadas del punto de intersección consiste en establecer un sistema de ecuaciones a partir de las ecuaciones de las rectas. En este caso, el sistema de ecuaciones a partir de las ecuaciones de las rectas \(L_1\) y \(L_2\) es: \[\begin{aligned}y&=3x-3\\y&=-x+1\end{aligned}\]
El segundo paso consiste en igualar las ecuaciones y despejar la incógnita \(x\) para encontrar su valor: \[\begin{aligned}3x-3&=-x+1\\3x+x&=1+3\\4x&=4\\x&=\frac{4}{4}\\x&=1\end{aligned}\] De esta manera, obtenemos que el valor de la coordenada \(x\) del punto de intersección \(P_0\) es \(x_0=1\).
El tercer paso consiste en sustituir el valor de la incógnita \(x\) en alguna de las dos ecuaciones de las rectas para obtener el valor de la incógnita \(y\). Al sustituir el valor de \(x=1\) en la ecuación de la recta \(L_1\), obtenemos que: \[\begin{aligned}y&=3x-3\\&=3(1)-3\\&=3-3\\&=0\end{aligned}\]. De esta manera, obtenemos que el valor de la coordenada \(y\) del punto de intersección \(P_0\) es \(y_0=0\).
Por lo tanto, las coordenadas del punto de intersección \(P_0\) de las rectas \(L_1\) y \(L_2\) son \(x_0=1\) y \(y_0=0\). En otras palabras, la recta \(L_1\) intercepta a la recta \(L_2\) en el punto \(P_0\) de coordenadas \((1,0)\). La siguiente imagen muestra el punto de intersección de las dos rectas en el plano cartesiano.
Ejemplo 2. Calcula el punto de intersección de las rectas \(L_1\) y \(L_2\) definidas por las siguientes ecuaciones: \[\begin{aligned}y&=2x+1\\y&=-3x+5\end{aligned}\]
Solución: El primer paso para hallar las coordenadas del punto de intersección de dos rectas consiste en definir un sistema de ecuaciones a partir de las ecuaciones de las rectas. En este caso, el sistema de ecuaciones a partir de las ecuaciones de las rectas \(L_1\) y \(L_2\) es: \[\begin{aligned}y&=2x+1\\y&=-3x+5\end{aligned}\]
El segundo paso consiste en igualar las ecuaciones y despejar la incógnita \(x\) para encontrar su valor: \[\begin{aligned}2x+1&=-3x+5\\2x+3x&=5-1\\5x&=4\\x&=\frac{4}{5}\end{aligned}\] De esta manera, obtenemos que el valor de la coordenada \(x\) del punto de intersección \(P\) es \(x_0=\frac{4}{5}\).
El tercer paso consiste en sustituir el valor de la incógnita \(x\) en alguna de las dos ecuaciones de las rectas para obtener el valor de la incógnita \(y\). Al sustituir el valor de \(x=\frac{4}{5}\) en la ecuación de la recta \(L_1\), obtenemos que: \[\begin{aligned}y&=2x+1\\&=2\left(\frac{4}{5}\right)+1\\&=\frac{8}{5}+1\\&=\frac{13}{5}\end{aligned}\]. Así, obtenemos que el valor de la coordenada \(y\) del punto de intersección \(P\) es \(y_0=\frac{13}{5}\).
Por lo tanto, el punto de intersección de las dos rectas \(L_1\) y \(L_2\) tiene las coordenadas \(\left(\frac{4}{5}, \frac{13}{5}\right)\). En otras palabras, la recta \(L_1\) interseca la recta \(L_2\) en el punto \(P\) de coordenadas \(\left(\frac{4}{5}, \frac{13}{5}\right)\). La siguiente imagen muestra el punto de intersección de las rectas.
Ejemplo 3. Encuentra el punto de intersección de dos rectas definidas por las ecuaciones: \[\begin{aligned}y&=1-2x\\y&=3x+6\end{aligned}\]
Solución: Al igualar las ecuaciones, obtenemos: \[1-2x=3x+6\] Resolviendo para la incógnita \(x\), obtenemos que: \[\begin{aligned}1-2x&=3x+6\\-2x-3x&=6-1\\-5x&=5\\x&=\frac{5}{-5}\\&=-1\end{aligned}\]. De esta manera, tenemos que el valor de la coordenada \(x\) del punto de intersección \(P\) es \(x_0=-1\).
Sustituyendo \(x=-1\) en la ecuación de la recta \(L_1\), obtenemos: \[\begin{aligned}y&=1-2x\\&=1-2(-1)\\&=1+2\\&=3\end{aligned}\]. Así, obtenemos que el valor de la coordenada \(y\) del punto de intersección \(P\) es \(y_0=3\). Por lo tanto, el punto de intersección de las dos rectas \(L_1\) y \(L_2\) tiene las coordenadas \((-1, 3)\). La siguiente imagen muestra las rectas en el plano cartesiano y el punto donde éstas se interceptan.
Hasta ahora, hemos visto cómo calcular el punto de intersección de dos rectas a partir de sus ecuaciones en la forma pendiente-ordenada al origen (\(y=mx+b\)). A continuación, veamos cómo encontrar el punto de intersección de dos rectas a partir de sus ecuaciones en la forma general (\(Ax+By+C=0\)).
Ecuación en la forma general
Si las ecuaciones de las rectas \(L_1\) y \(L_2\) se encuentran en la forma general: \[Ax+By+C=0\] es decir, si la recta \(L_1\) está definida por la ecuación \[A_1x+B_1y+C_1=0\] y la recta \(L_2\) está definida por la ecuación \[A_2x+B_2y+C_2=0\] entonces el punto \(P_0\) de coordenadas \((x_0, y_0)\) es el punto de intersección de las rectas \(L_1\) y \(L_2\) si los valores de las coordenadas \(x_0\) y \(y_0\) satisfacen ambas ecuaciones de las rectas simultáneamente.
Los valores de \(x_0\) y \(y_0\) se obtienen al resolver el sistema de dos ecuaciones con dos incógnitas definido por las ecuaciones de las rectas en la forma general. La técnica para hallar los valores de las coordenadas consiste en realizar operaciones entre ambas ecuaciones para anular una de las dos variables.
A continuación, presentamos algunos ejemplos de cómo calcular el punto de intersección entre dos rectas a partir de sus ecuaciones en la forma general.
Intersección de dos rectas en la forma general ejemplos
Ejemplo 4. Calcula el punto de intersección entre las rectas \(L_1\) y \(L_2\) definidas por las siguientes ecuaciones en su forma general: \[\begin{aligned}2x+2y-1&=0\\-2x+y+4&=0\end{aligned}\]
Solución: El primer paso para hallar los valores de las coordenadas del punto de intersección consiste en establecer un sistema de ecuaciones a partir de las ecuaciones de las rectas. En este caso, el sistema de ecuaciones a partir de las ecuaciones de las rectas \(L_1\) y \(L_2\) es: \[\begin{aligned}2x+2y-1&=0\\-2x+y+4&=0\end{aligned}\]
El segundo paso consiste en efectuar operaciones entre ambas ecuaciones para anular una de las dos variables en una de las dos ecuaciones. En este caso, observa que el término \(2x\) aparece en ambas ecuaciones, pero con signo contrario, es decir, en una ecuación aparece con signo positivo y en la otra aparece con signo negativo. Al sumar ambas ecuaciones, se obtiene una ecuación sin este término y con una sola variable. Es decir, al sumar ambas ecuaciones, obtenemos:
La ecuación resultante es: \[3y+3=0\] Observa que esta es una ecuación de una sola incógnita, en este caso \(y\). Al resolver para \(y\), obtenemos: \[\begin{aligned}3y+3&=0\\3y&=-3\\y&=\frac{-3}{3}\\&=-1\end{aligned}\] De esta manera, obtenemos que el valor de la coordenada vertical \(y\) del punto de intersección \(P_0\) es \(y_0=-1\).
El tercer paso consiste en sustituir el valor de la variable encontrada en alguna de las dos ecuaciones de las rectas para encontrar el valor de la variable faltante. En este caso, tenemos que \(y=-1\). Al sustituir este valor en la ecuación de la recta \(L_1\), obtenemos el valor de la variable \(x\): \[\begin{aligned}2x+2y-1&=0\\2x+2(-1)-1&=0\\2x-2-1&=0\\2x-3&=0\\2x&=3\\x&=\frac{3}{2}\end{aligned}\] De esta manera, obtenemos que el valor de la coordenada \(x\) del punto de intersección \(P_0\) es \(x_0=\frac{3}{2}\).
Por lo tanto, las coordenadas del punto de intersección \(P_0\) de las rectas \(L_1\) y \(L_2\) son \(x_0=\frac{3}{2}\) y \(y_0=-1\). En otras palabras, la recta \(L_1\) intercepta a la recta \(L_2\) en el punto \(P_0\) de coordenadas \(\left(\frac{3}{2}, -1\right)\). La siguiente imagen muestra las rectas en el plano y el punto donde éstas se interceptan.
Preguntas frecuentes
¿Qué es el punto de intersección de dos rectas? El punto de intersección de dos rectas es el punto \(P\) de coordenadas \((x, y)\) donde las rectas se cortan.