Producto vectorial: Producto cruz de dos vectores

Producto vectorial o producto cruz

El producto vectorial, también conocido como producto cruz, es una operación que nos permite obtener un nuevo vector que es perpendicular a los vectores que se multiplican. A diferencia del producto punto, que da como resultado un número, el producto vectorial nos brinda un vector que posee propiedades geométricas únicas. En esta entrada, exploráremos en detalle qué es el producto vectorial, sus propiedades clave, cómo se calcula y algunas de sus aplicaciones más relevantes.

Producto Vectorial

El producto vectorial o producto cruz de dos vectores \(\vec{A}\) y \(\vec{B}\) se denota por: \[\vec{C}=\vec{A}\times\vec{B}\]

Se lee: \(\vec{A}\) cruz \(\vec{B}\). La magnitud del vector resultante \(\vec{C}\) es igual al producto de las magnitudes de los vectores \(\vec{A}\) y \(\vec{B}\) por el seno del ángulo \(\theta\) entre ellos.

La dirección del vector \(\vec{C}\) es perpendicular al plano formado por los vectores \(\vec{A}\) y \(\vec{B}\), de modo que los vectores \(\vec{A}\), \(\vec{B}\) y \(\vec{C}\) forman un sistema de mano derecha. Es decir:

\[\vec{A}\times\vec{B}=|A||B|\sin{\theta}\hat{u}\]

Donde \(\hat{u}\) es un vector unitario que indica la dirección del vector resultante \(\vec{C}\).

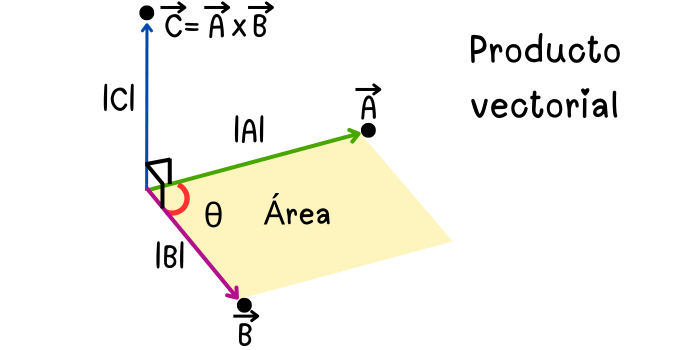
La magnitud del vector \(\vec{C}\) también se puede interpretar como el área de un paralelogramo con lados \(\vec{A}\) y \(\vec{B}\). Esto lo veremos con mayor detalle luego de conocer la propiedad del área de un paralelogramo.

Propiedades del producto cruz

Sean \(\vec{A}\), \(\vec{B}\) y \(\vec{C}\) vectores y \(m\) un escalar, tal que el producto cruz cumple las siguientes propiedades:

Propiedad NO conmutativa del producto cruz

Propiedad 1. Propiedad NO conmutativa del producto punto: \[\vec{A}\times\vec{B}\neq\vec{B}\times\vec{A}\] Esta propiedad establece que el producto cruz no es conmutativo, es decir, el orden en el que se realiza el producto cruz es importante. Sin embargo, lo que se si se cumple es que:

\[\vec{A}\times\vec{B}=-\left(\vec{B}\times\vec{A}\right)\]

Propiedad distributiva del producto cruz

Propiedad 2. Propiedad distributiva del producto cruz:

\[\vec{A}\times\left(\vec{B}+\vec{C}\right)=\vec{A}\times\vec{B}+\vec{A}\times\vec{C}\]

Esta propiedad establece que el producto cruz es distributivo, es decir, el producto cruz entre un vector y una suma de vectores, es igual a la suma de los productos cruz de dicho vector con cada uno de los sumandos.

Propiedad asociativa del producto cruz

Propiedad 3. Propiedad asociativa del producto cruz:

\[\begin{aligned}m\left(\vec{A}\times\vec{B}\right)&=\left(m\vec{A}\right)\times\vec{B}\\&=\vec{A}\times\left(m\vec{B}\right)\\&=\left(\vec{A}\times\vec{B}\right)m\end{aligned}\]

Producto cruz de vectores unitarios

Propiedad 4. Producto cruz de los vectores unitarios: \(\vec{i}\), \(\vec{j}\) y \(\vec{k}\).

\[\begin{aligned}\vec{i}\times\vec{i}&=0\\\vec{j}\times\vec{j}&=0\\\vec{k}\times\vec{k}&=0\\\vec{i}\times\vec{j}&=\vec{k}\\\vec{j}\times\vec{k}&=\vec{i}\\\vec{k}\times\vec{i}&=\vec{j}\end{aligned}\]

Producto cruz de vectores paralelos

Propiedad 5. Producto cruz de vectores paralelos: Si \(\vec{A}\) y \(\vec{B}\) son vectores diferentes al vector nulo y además se cumple que: \[\vec{A}\times\vec{B}=0\] Entonces los vectores \(\vec{A}\) y \(\vec{B}\) son paralelos. Esta propiedad establece simplemente que si dos vectores no son iguales al vector nulo y su producto cruz es igual a cero, entonces estos vectores son paralelos.

Área de un paralelogramo

Propiedad 6. Área de un paralelogramo a partir del producto cruz de dos vectores. La magnitud del vector \(\vec{C}\), donde \(\vec{C}=\vec{A}\times\vec{B}\), corresponde al área del paralelogramo delimitado por los vectores \(\vec{A}\) y \(\vec{B}\). Esta propiedad establece que se puede hallar el área de un paralelogramo a partir de la magnitud (longitud) del vector que resulta de realizar el producto cruz de los dos vectores que delimitan el área del paralelogramo.

Regla de la mano derecha

La regla de la mano derecha es una herramienta útil para determinar la dirección del vector resultante al realizar el producto vectorial. Esta regla establece que, si colocas el dedo pulgar de tu mano derecha en la dirección del primer vector y los dedos restantes en la dirección del segundo vector, el vector resultante será perpendicular al plano formado por los dedos restantes, es decir, será la dirección apuntada por el dedo pulgar.

Aquí tienes una descripción detallada de cómo aplicar la regla de la mano derecha: Si extendemos la mano derecha con los dedos apuntando en dirección del primer vector, que este caso es \(\vec{u}\) y luego curvamos los dedos hacia el segundo vector, que es este caso es \(\vec{v}\), el pulgar apunta en la dirección del producto vectorial \(\vec{u}\times\vec{v}\). Este procedimiento se muestra en la siguiente figura.

¿Cómo aplicar la regla de la mano derecha para hallar la dirección del producto vectorial?

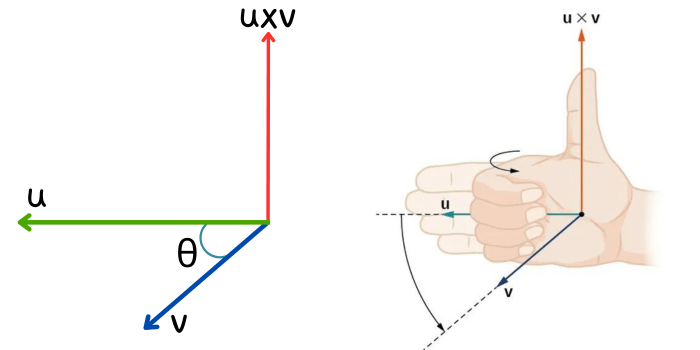
Es importante tener en cuenta que la regla de la mano derecha proporciona la dirección, pero no la magnitud del vector resultante. Esta regla es especialmente útil cuando se trabaja con vectores en el espacio tridimensional, ya que permite visualizar de manera intuitiva la dirección del vector resultante.

Producto cruz de vectores usando sus componentes

Existe una fórmula sencilla para realizar el producto cruz entre dos vectores \(\vec{A}\) y \(\vec{B}\) cuando se usan los vectores unitarios \(\vec{i}\), \(\vec{j}\) y \(\vec{k}\). Sean los vectores \(\vec{A}\) y \(\vec{B}\) definidos como: \[\begin{aligned}\vec{A}&=\left(A_{1}\vec{i}+A_{2}\vec{j}+A_{3}\vec{k}\right)\\\vec{B}&=\left(B_{1}\vec{i}+B_{2}\vec{j}+B_{3}\vec{k}\right)\end{aligned}\] Entonces:

\[\begin{aligned}\vec{A}\times\vec{B}&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\A_{1}&A_{2}&A_{3}\\B_{1}&B_{2}&B_{3}\end{vmatrix}\\\\&=\begin{vmatrix}A_{2}&A_{3}\\B_{2}&B_{3}\end{vmatrix}\vec{i}-\begin{vmatrix}A_{1}&A_{3}\\B_{1}&B_{3}\end{vmatrix}\vec{j}+\begin{vmatrix}A_{1}&A_{2}\\B_{1}&B_{2}\end{vmatrix}\vec{k}\end{aligned}\]

Producto cruz ejercicios resueltos

Ejercicio 1. Calcular el producto cruz de los vectores \(\vec{A}\) y \(\vec{B}\) definidos por: \[\begin{aligned}\vec{A}&=1\vec{i}+2\vec{j}+3\vec{k}\\B&=-1\vec{i}+1\vec{j}+2\vec{k}\end{aligned}\] Solución:

\[\begin{aligned}\vec{A}\times\vec{B}&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\A_{1}&A_{2}&A_{3}\\B_{1}&B_{2}&B_{3}\end{vmatrix}\\\\&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\1&2&3\\-1&1&2\end{vmatrix}\\\\&=\begin{vmatrix}2&3\\1&2\end{vmatrix}\vec{i}-\begin{vmatrix}1&3\\-1&2\end{vmatrix}\vec{j}+\begin{vmatrix}1&2\\-1&1\end{vmatrix}\vec{k}\\\\&=\left[(2)(2)-(3)(1)\right]\vec{i}-\left[(1)(2)-(3)(-1)\right]\vec{j}+\left[(1)(1)-(2)(-1)\right]\vec{k}\\\\&=\left[4-3\right]\vec{i}-\left[2-(-3)\right]\vec{j}+\left[1-(-2)\right]\vec{k}\\\\&=\left[1\right]\vec{i}-\left[2+3\right]\vec{j}+\left[1+2\right]\vec{k}\\\\&=1\vec{i}-5\vec{j}+3\vec{k}\end{aligned}\]

Ejercicio 2. Calcular el producto cruz de los vectores \(\vec{A}\) y \(\vec{B}\) definidos como: \[\begin{aligned}\vec{A}&=\vec{j}+2\vec{k}\\\vec{B}&=\vec{i}+2\vec{j}+3\vec{k}\end{aligned}\] Solución:

\[\begin{aligned}\vec{A}\times\vec{B}&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\A_{1}&A_{2}&A_{3}\\B_{1}&B_{2}&B_{3}\end{vmatrix}\\\\&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\0&1&2\\1&2&3\end{vmatrix}\\\\&=\begin{vmatrix}1&2\\2&3\end{vmatrix}\vec{i}-\begin{vmatrix}0&2\\1&3\end{vmatrix}\vec{j}+\begin{vmatrix}0&1\\1&2\end{vmatrix}\vec{k}\\\\&=\left[(1)(3)-(2)(2)\right]\vec{i}-\left[(0)(3)-(2)(1)\right]\vec{j}+\left[(0)(2)-(1)(1)\right]\vec{k}\\\\&=\left[3-4\right]\vec{i}-\left[0-2\right]\vec{j}+\left[0-1\right]\vec{k}\\\\&=\left[-1\right]\vec{i}-\left[-2\right]\vec{j}+\left[-1\right]\vec{k}\\\\&=-1\vec{i}+2\vec{j}-1\vec{k}\end{aligned}\]

Ejercicio 3. Dados los vectores \(\vec{A}\), \(\vec{B}\) y \(\vec{C}\): \[\begin{aligned}\vec{A}&=-\vec{i}+\vec{j}+\vec{k}\\B&=\vec{i}-\vec{j}+\vec{k}\\\vec{C}&=\vec{i}+\vec{j}-\vec{k}\end{aligned}\] Calcular \(\left(\vec{A}\times\vec{B}\right)\times\vec{C}\)

Solución: Primero debemos hallar el producto cruz que se encuentra dentro de los paréntesis, con el vector que resulte haremos el siguiente producto cruz para hallar el resultado final.

\[\begin{aligned}\vec{A}\times\vec{B}&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\A_{1}&A_{2}&A_{3}\\B_{1}&B_{2}&B_{3}\end{vmatrix}\\\\&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\-1&1&1\\1&-1&1\end{vmatrix}\\\\&=\begin{vmatrix}1&1\\-1&1\end{vmatrix}\vec{i}-\begin{vmatrix}-1&1\\1&1\end{vmatrix}\vec{j}+\begin{vmatrix}-1&1\\1&-1\end{vmatrix}\vec{k}\\\\&=\left[(1)(1)-(1)(-1)\right]\vec{i}-\left[(-1)(1)-(1)(1)\right]\vec{j}+\left[(-1)(-1)-(1)(1)\right]\vec{k}\\\\&=\left[1-(-1)\right]\vec{i}-\left[-1-1\right]\vec{j}+\left[1-1\right]\vec{k}\\\\&=\left[1+1\right]\vec{i}-\left[-2\right]\vec{j}+\left[0\right]\vec{k}\\\\&=2\vec{i}+2\vec{j}\end{aligned}\]

\[\begin{aligned}\left(\vec{A}\times\vec{B}\right)\times\vec{C}&=\left(2\vec{i}+2\vec{j}\right)\times\left(\vec{i}+\vec{j}-\vec{k}\right)\\&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\2&2&0\\1&1&-1\end{vmatrix}\\\\&=\begin{vmatrix}2&0\\1&-1\end{vmatrix}\vec{i}-\begin{vmatrix}2&0\\1&-1\end{vmatrix}\vec{j}+\begin{vmatrix}2&2\\1&1\end{vmatrix}\vec{k}\\\\&=\left[(2)(-1)-(0)(1)\right]\vec{i}-\left[(2)(-1)-(0)(1)\right]\vec{j}+\left[(2)(1)-(2)(1)\right]\vec{k}\\\\&=\left[-2-0\right]\vec{i}-\left[-2-0\right]\vec{j}+\left[2-2\right]\vec{k}\\\\&=\left[-2\right]\vec{i}-\left[-2\right]\vec{j}+\left[0\right]\vec{k}\\\\&=-2\vec{i}+2\vec{j}\end{aligned}\]

Ejercicio 4. Hallar un vector unitario perpendicular al plano formado por los vectores \(\vec{A}\) y \(\vec{B}\) definidos como: \[\begin{aligned}\vec{A}&=2\vec{i}-6\vec{j}-3\vec{k}\\B&=4\vec{i}+3\vec{j}-\vec{k}\end{aligned}\]

Solución: Para hallar un vector unitario que sea perpendicular al plano formado por los vectores \(\vec{A}\) y \(\vec{B}\), primero debemos hallar el vector perpendicular, este lo podemos determinar simplemente al realizar el producto cruz entre \(\vec{A}\) y \(\vec{B}\). Recuerda que por definición el producto cruz entre dos vectores da como resultado un vector perpendicular a estos. Entonces:

\[\begin{aligned}\vec{A}\times\vec{B}&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\A_{1}&A_{2}&A_{3}\\B_{1}&B_{2}&B_{3}\end{vmatrix}\\\\&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\2&-6&-3\\4&3&-1\end{vmatrix}\\\\&=\begin{vmatrix}-6&-3\\3&-1\end{vmatrix}\vec{i}-\begin{vmatrix}2&-3\\4&-1\end{vmatrix}\vec{j}+\begin{vmatrix}2&-6\\4&3\end{vmatrix}\vec{k}\\\\&=\left[(-6)(-1)-(-3)(3)\right]\vec{i}-\left[(2)(-1)-(-3)(4)\right]\vec{j}+\left[(2)(3)-(-6)(4)\right]\vec{k}\\\\&=\left[6-(-9)\right]\vec{i}-\left[-2-(-12)\right]\vec{j}+\left[6-(-24)\right]\vec{k}\\\\&=\left[6+9\right]\vec{i}-\left[-2+12\right]\vec{j}+\left[6+24\right]\vec{k}\\\\&=15\vec{i}-10\vec{j}+30\vec{k}\end{aligned}\]

Para hallar un vector unitario simplemente debemos dividir al vector entre su magnitud. En nuestro caso el vector es el resultado de realizar un producto cruz entre los vectores \(\vec{A}\) y \(\vec{B}\), por lo tanto el vector unitario está definido como:

\[\frac{\vec{A}\times\vec{B}}{|\vec{A}\times\vec{B}|}\]

Como ya conocemos al vector \(\vec{A}\times\vec{B}\), ahora simplemente debemos hallar su magnitud:

\[\begin{aligned}|\vec{A}\times\vec{B}|&=\sqrt{15^2+(-10)^2+30^2}\\&=\sqrt{225+100+900}\\&=\sqrt{1225}\\&=35\end{aligned}\]

Por lo tanto, un vector unitario perpendicular al plano formado por los vectores \(\vec{A}\) y \(\vec{B}\) es:

\[\begin{aligned}\frac{\vec{A}\times\vec{B}}{|\vec{A}\times\vec{B}|}&=\frac{15\vec{i}-10\vec{j}+30\vec{k}}{35}\\&=\frac{3}{7}\vec{i}-\frac{2}{7}\vec{j}+\frac{6}{7}\vec{k}\end{aligned}\]

Ejercicio 5. Calcular el área del triángulo cuyos vértices están en los puntos \(P\), \(Q\) y \(R\) definidos como: \[\begin{aligned}P&(1, 3, 2)\\Q&(2, -1, 1)\\R&(-1, 2, 3)\end{aligned}\]

Solución: Para hallar el área del triángulo primero debemos recordar que la magnitud del producto cruz entre dos vectores \(\vec{A}\) y \(\vec{B}\) se puede interpretar como el área del paralelogramo formado por estos vectores. Además el área de un triángulo corresponde a la mitad del área del paralelogramo, es decir: \[\text{Área}=\frac{1}{2}|\vec{A}\times\vec{B}|\] Como conocemos los tres vértices del triángulo, simplemente debemos definir dos vectores que partan desde un mismo vértice hacia los otros dos, es decir:

\[\begin{aligned}\vec{PQ}&=(2-1)\vec{i}+(-1-3)\vec{j}+(1-2)\vec{k}\\&=1\vec{i}-4\vec{j}-1\vec{k}\\\vec{PR}&=(-1-1)\vec{i}+(2-3)\vec{j}+(3-2)\vec{k}\\&=-2\vec{i}-1\vec{j}+1\vec{k}\end{aligned}\]

Ahora que conocemos los vectores debemos hallar el producto cruz:

\[\begin{aligned}\vec{PQ}\times\vec{PR}&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\1&-4&-1\\-2&-1&1\end{vmatrix}\\\\&=\begin{vmatrix}-4&-1\\-1&1\end{vmatrix}\vec{i}-\begin{vmatrix}1&-1\\-2&1\end{vmatrix}\vec{j}+\begin{vmatrix}1&-4\\-2&-1\end{vmatrix}\vec{k}\\\\&=\left[(-4)(1)-(-1)(-1)\right]\vec{i}-\left[(1)(1)-(-1)(-2)\right]\vec{j}+\left[(1)(-1)-(-4)(-2)\right]\vec{k}\\\\&=\left[-4-1\right]\vec{i}-\left[1-2\right]\vec{j}+\left[-1-8\right]\vec{k}\\\\&=\left[-5\right]\vec{i}-\left[-1\right]\vec{j}+\left[-9\right]\vec{k}\\\\&=-5\vec{i}+1\vec{j}-9\vec{k}\end{aligned}\]

Como necesitamos la magnitud de este vector, entonces procedemos a calcularlo:

\[\begin{aligned}|\vec{PQ}\times\vec{PR}|&=\sqrt{(-5)^2+(1)^2+(-9)^2}\\&=\sqrt{25+1+81}\\&=\sqrt{107}\end{aligned}\]

Por lo tanto, el área del triángulo es:

\[\begin{aligned}\frac{1}{2}|\vec{PQ}\times\vec{PR}|&=\frac{1}{2}\sqrt{107}\end{aligned}\]