Distancia entre dos puntos: Fórmula y ejemplos

Distancia entre dos puntos

La distancia entre dos puntos se define como la longitud del segmento de recta que une los puntos.

Distancia entre dos puntos fórmula

La fórmula para hallar la distancia entre dos puntos en el plano cartesiano es:

\[d(A, B)=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\]

A continuación, veremos cómo deducir esta fórmula, las variantes en la fórmula, y presentaremos una serie de ejemplos resueltos paso a paso junto con ejercicios para practicar el tema.

Deducción de la fórmula para hallar la distancia entre dos puntos

Para deducir la expresión matemática que nos permita hallar la distancia entre dos puntos, nos apoyaremos en el plano cartesiano y aplicaremos el teorema de Pitágoras. Para esto, sean \(A\) y \(B\) dos puntos en el plano cartesiano cuyas coordenadas son \((x_{1}, y_{1})\) y \((x_{2}, y_{2})\) respectivamente. La siguiente imagen muestra una posible ubicación de estos puntos en el plano.

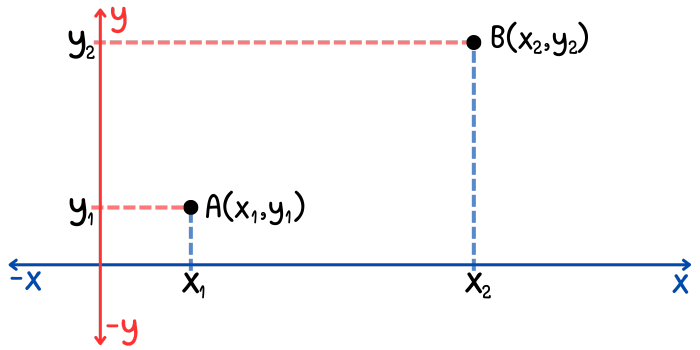
Si unimos estos puntos con una línea recta desde el punto \(A\) hasta el punto \(B\), la longitud de esta recta representará la distancia entre estos puntos. La distancia entre el punto \(A\) y el punto \(B\) se escribe como: \(d(A, B)\). Para hallar la longitud de esta recta, primero trazamos una línea recta paralela al eje \(x\), cuya longitud es: \(x_{2}-x_{1}\) (diferencia de abscisas) y luego trazamos una línea recta paralela al eje \(y\) cuya longitud es: \(y_{2}-y_{1}\) (diferencia de ordenadas), esto con el objetivo de formar un triángulo rectángulo y poder aplicar el teorema de Pitágoras.

Fórmula para hallar la distancia entre dos puntos

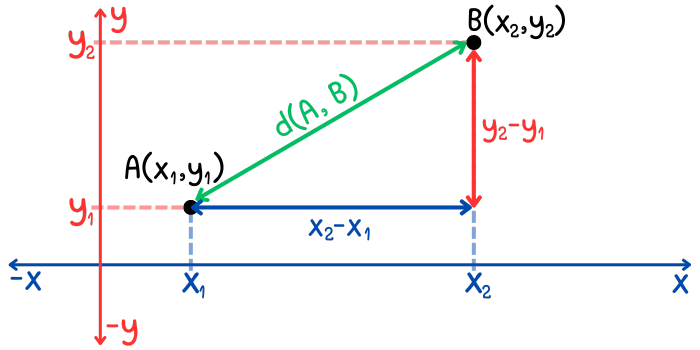
El teorema de Pitágoras establece que el cuadrado de la longitud de la hipotenusa de un triángulo rectángulo es igual a la suma de los cuadrados de la longitud de sus catetos. Aplicando este teorema al triángulo rectángulo de la imagen, obtenemos:

\[\left(d(A, B)\right)^2=\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2\]

Para obtener \(d(A, B)\), simplemente debemos aplicar raíz cuadrada en ambos miembros de la igualdad:

\[\begin{aligned}\sqrt{\left(d(A, B)\right)^2}&=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\\d(A, B)&=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\end{aligned}\]

Por lo tanto, la fórmula para hallar la distancia entre dos puntos es:

\[d(A, B)=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\]

La distancia entre dos puntos siempre es mayor o igual a cero, en otras palabras, siempre es positiva. Al hallar una longitud se debe indicar la unidad de medición con la que se está trabajando, por ejemplo: centímetros, metros, kilómetros, etc. En caso de no conocer las unidades, el resultado se expresa simplemente como el valor numérico acompañado de la frase "unidades de longitud".

Distancia entre dos puntos: Horizontal, vertical y oblicua

Hay tres formas diferentes en las que dos puntos pueden estar ubicados en el plano cartesiano:

Horizontal: Los puntos se encuentran sobre una misma recta horizontal.
Vertical: Los puntos se encuentran sobre una misma recta vertical.
Oblicua: Los puntos se encuentran sobre una misma recta inclinada.

En cada uno de estos casos, la fórmula para hallar la distancia entre los puntos es diferente.

Distancia entre dos puntos horizontal

La fórmula para hallar la distancia entre dos puntos que se encuentran sobre una misma recta horizontal es:

\[d(A, B)=|x_{2}-x_{1}|\]

Veamos cómo se obtiene esta fórmula. Dos puntos, \(A\) y \(B\), están sobre una misma recta horizontal si su coordenada \(y\) es la misma. Sean \(A\) y \(B\) dos puntos en el plano cartesiano cuyas coordenadas son \((x_{1}, y_{1})\) y \((x_{2}, y_{1})\) respectivamente. Observa que ambos puntos tienen la misma coordenada \(y_{1}\). La siguiente imagen muestra la ubicación de estos puntos en el plano cartesiano.

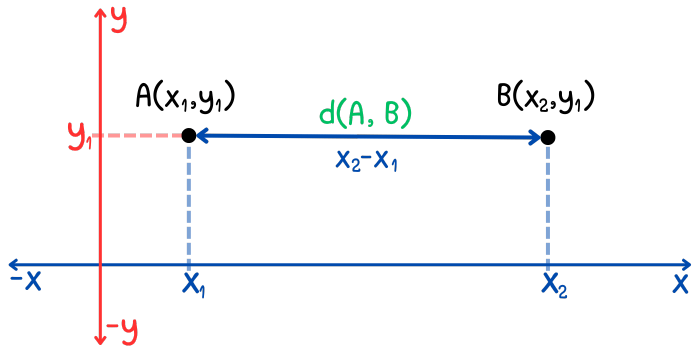
Aplicando la fórmula para hallar la distancia entre dos puntos, obtenemos:

\[\begin{aligned}d(A, B)&=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\\&=\sqrt{(x_{2}-x_{1})^2+(y_{1}-y_{1})^2}\\&=\sqrt{(x_{2}-x_{1})^2+0^2}\\&=\sqrt{(x_{2}-x_{1})^2}\\&=|x_{2}-x_{1}|\end{aligned}\]

Es decir, la distancia entre dos puntos alineados horizontalmente corresponde al valor absoluto de la diferencia de sus abscisas.

Distancia entre dos puntos horizontal ejemplos

Ejemplo 1. Hallar la distancia entre los puntos \(A\) y \(B\) cuyas coordenadas son: \[\begin{aligned}A&(2, 5)\\B&(8, 5)\end{aligned}\]

Solución: Para hallar la distancia entre los puntos \(A\) y \(B\), primero debes observar que la coordenada \(y\) de ambos puntos es la misma, esto quiere decir que ambos puntos están alineados horizontalmente (se encuentran sobre una misma recta horizontal), por lo tanto, la distancia entre ambos se calcula simplemente como: \[d(A, B)=|x_{2}-x_{1}|\] Sustituyendo los valores de las abscisas obtenemos: \[\begin{aligned} d(A, B)&=|x_{2}-x_{1}|\\&=|8-2|\\&=|6|\\&=6\end{aligned}\]

Por lo tanto, la distancia entre \(A\) y \(B\) es igual a 6 unidades de longitud.

Distancia entre dos puntos vertical

La fórmula para hallar la distancia entre dos puntos que se encuentran sobre una misma recta vertical es:

\[d(A, B)=|y_{2}-y_{1}|\]

Veamos cómo se obtiene esta fórmula. Dos puntos \(A\) y \(B\), están sobre una misma recta vertical si su coordenada \(x\) es la misma. Sean \(A\) y \(B\) dos puntos en el plano cartesiano cuyas coordenadas son \((x_{1}, y_{1})\) y \((x_{1}, y_{2})\) respectivamente. Observa que ambos puntos tienen la misma coordenada \(x_{1}\). La siguiente imagen muestra la ubicación de estos puntos en el plano cartesiano.

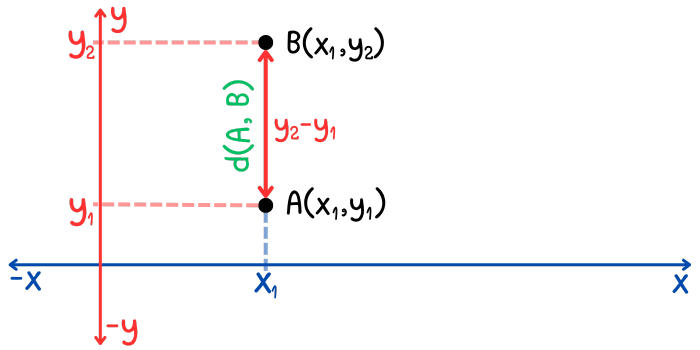
Aplicando la fórmula para hallar la distancia entre dos puntos, obtenemos:

\[\begin{aligned}d(A, B)&=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\\&=\sqrt{(x_{1}-x_{1})^2+(y_{2}-y_{1})^2}\\&=\sqrt{0^2+(y_{2}-y_{1})^2}\\&=\sqrt{(y_{2}-y_{1})^2}\\&=|y_{2}-y_{1}|\end{aligned}\]

Es decir, la distancia entre dos puntos alineados verticalmente corresponde al valor absoluto de la diferencia de sus ordenadas.

Distancia entre dos puntos vertical ejemplos

Ejemplo 2. Calcular la distancia entre los puntos \(A\) y \(B\) cuyas coordenadas son: \[\begin{aligned}A&(3, 9)\\B&(3, -2)\end{aligned}\]

Solución: Primero observa que la coordenada en \(x\) de ambos puntos es la misma, esto quiere decir que ambos puntos se encuentran alineados verticalmente (se encuentran sobre una misma recta vertical), por lo tanto, la distancia entre ambos puntos se calcula simplemente como: \[d(A, B)=|y_{2}-y_{1}|\] Sustituyendo los valores de las ordenadas obtenemos: \[\begin{aligned} d(A, B)&=|y_{2}-y_{1}|\\&=|-2-9|\\&=|-11|\\&=11\end{aligned}\]

Por lo tanto, la distancia entre \(A\) y \(B\) es igual a 11 unidades de longitud.

Distancia entre dos puntos oblicua

La distancia entre dos puntos que se encuentran sobre una misma recta oblicua (inclinada) está dada por:

\[d(A, B)=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\]

La deducción de esta ecuación es la que realizamos al inicio del post. Esta ecuación es la más usada cuando se desea hallar la distancia entre dos puntos, esto debido a que no siempre los puntos se encuentran alineados horizontal o verticalmente en el plano cartesiano.

Distancia entre dos puntos oblicua ejemplos

Ejemplo 3. Calcular la distancia entre los puntos \(A\) y \(B\) cuyas coordenadas son \[\begin{aligned}A&(-3, 5)\\B&(2, 4)\end{aligned}\]

Solución. Primero escribimos las coordenadas de los puntos en la forma \((x, y)\), es decir: \[\begin{aligned}(x_{1}, y_{1})&=(-3, 5)\\(x_{2}, y_{2})&=(2, 4)\end{aligned}\] Sustituyendo estos valores en la fórmula para hallar la distancia entre dos puntos, obtenemos:

\[\begin{aligned} d(A, B)&=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\\&=\sqrt{(2-(-3))^2+(4-5)^2}\\&=\sqrt{(2+3)^2+(4-5)^2}\\&=\sqrt{5^2+(-1)^2}\\&=\sqrt{25+1}\\&=\sqrt{26}\end{aligned}\]

Concluimos que la distancia entre los puntos \(A\) y \(B\) es igual a \(\sqrt{26}\) unidades de longitud.

Distancia entre dos puntos fórmula y ejemplos

Ejemplo 4. Calcular la distancia entre los puntos \(A\) y \(B\), cuyas coordenadas están definidas como: \[\begin{aligned}A&(3, 4)\\B&(7, 8)\end{aligned}\]

Solución. Primero escribimos las coordenadas de los puntos en la forma \((x, y)\), es decir: \[\begin{aligned}(x_{1}, y_{1})&=(3, 4)\\(x_{2}, y_{2})&=(7, 8)\end{aligned}\] Sustituyendo estos valores en la fórmula para hallar la distancia entre dos puntos, obtenemos:

\[\begin{aligned}d(A, B)&=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\\&=\sqrt{(7-3)^2+(8-4)^2}\\&=\sqrt{4^2+4^2}\\&=\sqrt{16+16}\\&=\sqrt{32}\end{aligned}\]

Concluimos que la distancia entre los puntos es igual a \(\sqrt{32}\) unidades de longitud.

Ejemplo 5. Hallar la distancia entre los puntos A y B, cuyas coordenadas son: \[\begin{aligned}A&(1, 3)\\B&(5, 6)\end{aligned}\]

Solución. Primero debemos escribir las coordenadas de los puntos en la forma \((x, y)\), es decir: \[\begin{aligned}(x_{1}, y_{1})&=(1, 3)\\(x_{2}, y_{2})&=(5, 6)\end{aligned}\] Recuerda que, la fórmula para hallar la distancia entre dos puntos es:

\[d(A, B)=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\]

Por lo tanto, al sustituir las coordenadas de los puntos en la fórmula, obtenemos:

\[\begin{aligned}d(A, B)&=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\\&=\sqrt{(5-)^2+(6-3)^2}\\&=\sqrt{4^2+3^2}\\&=\sqrt{16+9}\\&=\sqrt{25}\\&=5\end{aligned}\]

De esta manera concluimos que la distancia entre los puntos es igual a 5 unidades de longitud.

Ejemplo 6. Hallar la distancia desde el punto \(A\) al punto \(B\), cuyas coordenadas son: \[\begin{aligned}A&(-1, 7)\\B&(3, 4)\end{aligned}\]

Solución. Escribimos las coordenadas de los puntos en la forma \((x, y)\), es decir: \[\begin{aligned}(x_{1}, y_{1})&=(-1, 7)\\(x_{2}, y_{2})&=(3, 4)\end{aligned}\] La fórmula para hallar la distancia entre dos puntos es:

\[d(A, B)=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\]

Sustituyendo las coordenadas de los puntos en la fórmula, obtenemos:

\[\begin{aligned}d(A, B)&=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\\&=\sqrt{(3-(-1))^2+(4-7)^2}\\&=\sqrt{(3+1)^2+(-3)^2}\\&=\sqrt{4^2+(-3)^2}\\&=\sqrt{16+9}\\&=\sqrt{25}\\&=25\end{aligned}\]

Por lo tanto, la distancia entre los puntos es igual a 5 unidades de longitud.

Ejemplo 7. Hallar el perímetro del triángulo formado por los puntos A, B y C, cuyas coordenadas son: \[\begin{aligned}A&(2, 1)\\B&(5, 6)\\C&(7, 3)\end{aligned}\]

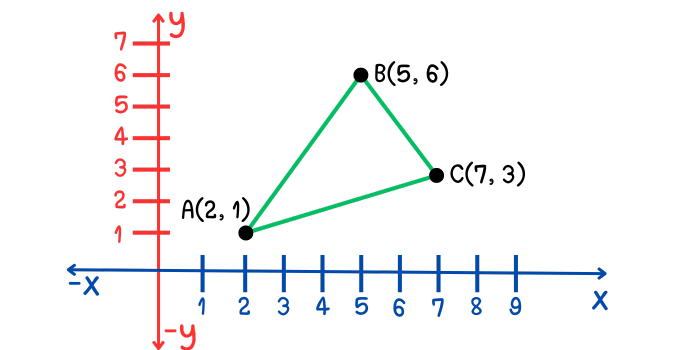
Solución. Primero debes recordar que el perímetro se define como la longitud del contorno de una figura. El perímetro de un triangulo es igual a la suma de las longitudes de sus tres lados. Hallar la longitud de los lados del triángulo es equivalente a hallar la distancia entre sus vértices. Recuerda que la fórmula para hallar la distancia entre dos puntos es:

\[d(A, B)=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\]

La longitud del segmente AB corresponde a la distancia desde el punto A hasta el punto B. Sustituyendo las coordenadas de estos puntos en la fórmula para hallar la distancia entre dos puntos, obtenemos:

\[\begin{aligned}d(A, B)&=\sqrt{(5-2)^2+(6-1)^2}\\&=\sqrt{3^2+5^2}\\&=\sqrt{9+25}\\&=\sqrt{34}\end{aligned}\]

La longitud del segmento BC corresponde a la distancia desde el punto B hasta el punto C. Sustituyendo las coordenadas de estos puntos en la fórmula para hallar la distancia entre dos puntos, obtenemos:

\[\begin{aligned}d(B, C)&=\sqrt{(7-5)^2+(3-6)^2}\\&=\sqrt{2^2+(-3)^2}\\&=\sqrt{4+9}\\&=\sqrt{13}\end{aligned}\]

La longitud del segmento CA corresponde a la distancia desde el punto C hasta el punto A. Sustituyendo las coordenadas de estos puntos en la fórmula para hallar la distancia entre dos puntos, obtenemos:

\[\begin{aligned}d(C, A)&=\sqrt{(2-7)^2+(1-3)^2}\\&=\sqrt{(-5)^2+(-2)^2}\\&=\sqrt{25+4}\\&=\sqrt{29}\end{aligned}\]

La suma de estas tres longitudes corresponde al perímetro del triángulo, es decir:

\[\begin{aligned}P&=d(A, B)+d(B, C)+d(C, A)\\&=\sqrt{34}+\sqrt{13}+\sqrt{29}\\&=14.82\end{aligned}\]

Por lo tanto, el perímetro del triángulo es igual a 14.82 unidades de longitud.

Ejemplo 8. Hallar el perímetro de un rectángulo cuyos vértices están representados por los puntos A, B, C y D, cuyas coordenadas son: \[\begin{aligned}A&(-2, 1)\\B&(-2, 4)\\C&(4, 4)\\D&(4, 1)\end{aligned}\]

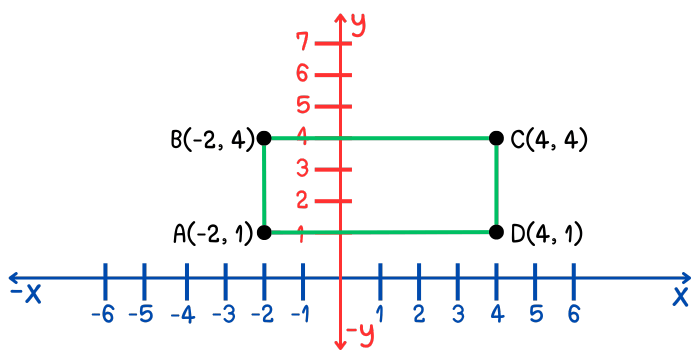
Solución. Primero debes recordar que el perímetro de un rectángulo es igual a dos veces la longitud de su base más dos veces la longitud de su altura, es decir: \[P=2b+2h\] Hallar la longitud de la base y la altura del rectángulo, es equivalente a hallar la distancia entre sus vértices. De acuerdo con la figura, el segmento AB corresponde a la altura del rectángulo y su longitud es igual a la distancia desde el punto A hasta el punto B. Como los puntos A y B se encuentran alineados verticalmente, entonces utilizamos la fórmula: \[d(A, B)=|y_{2}-y_{1}|\] Sustituyendo los valores de las ordenadas obtenemos: \[\begin{aligned}d(A, B)&=|y_{2}-y_{1}|\\&=|4-1|\\&=|3|\\&=3\end{aligned}\] De acuerdo con la figura, el segmento AD corresponde a la base del rectángulo y su longitud es igual a la distancia desde el punto A hasta el punto D. Como los puntos A y D se encuentran alineados horizontalmente, entonces utilizamos la fórmula: \[d(A, B)=|x_{2}-x_{1}|\] Sustituyendo los valores de las abscisas obtenemos: \[\begin{aligned}d(A, D)&=|x_{2}-x_{1}|\\&=|4-(-2)|\\&=|4+2|\\&=|6|\\&=6\end{aligned}\] Sustituyendo estos resultados en la fórmula para obtener el perímetro de un rectángulo, obtenemos: \[\begin{aligned}P&=2b+2h\\&=2(6)+2(3)\\&=12+6\\&=18\end{aligned}\] Por lo tanto, el perímetro del rectángulo es igual a 18 unidades de longitud.

Distancia entre dos puntos ejercicios para practicar

Los siguientes ejercicios te permitirán practicar el cálculo de distancias entre puntos en diferentes configuraciones: oblicuas, alineadas horizontalmente y alineadas verticalmente.

Ejercicio 1. Dadas las coordenadas de los puntos A y B en el plano cartesiano, encuentra la distancia entre ellos. \[\begin{aligned}A&(2, 3)\\B&(6, 5)\end{aligned}\]

Ejercicio 2. Encuentra la distancia entre los puntos C y D cuyas coordenadas son: \[\begin{aligned}C&(-1, 4)\\D&(3, -2)\end{aligned}\]

Ejercicio 3. Calcula la distancia entre los puntos E y F cuyas coordenadas son las siguientes: \[\begin{aligned}E&(0, 0)\\F&(0, 8)\end{aligned}\]

Ejercicio 4. Determina la distancia entre los puntos \[\begin{aligned}G&(5, 7)\\H&(5, 2)\end{aligned}\]

Ejercicio 5. Dados los puntos I y J, calcula la distancia entre ellos. \[\begin{aligned}I&(3, 6)\\J&(8, 6)\end{aligned}\]

Ejercicio 6. Encuentra la distancia entre los puntos \[\begin{aligned}K&(4, 3)\\L&(1, 7)\end{aligned}\]

Ejercicio 7. Calcula la distancia entre los puntos M y N cuyas coordenadas son: \[\begin{aligned}M&(2, -2)\\N&(2, 4)\end{aligned}\]

Ejercicio 8. Dados los puntos O y P , encuentra la distancia entre ellos. \[\begin{aligned}O&(0, 1)\\P&(7, 1)\end{aligned}\]

Ejercicio 9. Encuentra la distancia entre los siguientes dos puntos \[\begin{aligned}Q&(9, 5)\\R&(9, 11)\end{aligned}\]

Ejercicio 10. Calcula la distancia entre \[\begin{aligned}S&(4, 1)\\T&(4, 8)\end{aligned}\]

Distancia entre dos puntos preguntas frecuentes

¿Cómo se calcula la distancia entre dos puntos en un plano cartesiano? La distancia entre dos puntos \((x_1, y_1)\) y \((x_2, y_2)\) en un plano cartesiano se calcula utilizando la fórmula de la distancia euclidiana:

\[d(AB)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\]

¿Cuál es la fórmula para encontrar la distancia euclidiana entre dos puntos en un espacio tridimensional? En un espacio tridimensional, la distancia euclidiana entre dos puntos \((x_1, y_1, z_1)\) y \((x_2, y_2, z_2)\) se calcula con la siguiente fórmula:

\[d(AB)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}\]

¿Hay alguna diferencia entre la distancia y la magnitud de un vector? Sí, aunque ambos conceptos están relacionados, la distancia es un escalar que mide la separación entre dos puntos, mientras que la magnitud de un vector representa su longitud sin dirección. En algunos casos, la magnitud de un vector puede interpretarse como una distancia.

¿Cómo se aplica el concepto de distancia en problemas del mundo real, como la navegación o la logística? El concepto de distancia es esencial en problemas de navegación y logística para determinar la ruta más corta o eficiente entre dos puntos. Se utiliza en la planificación de rutas, transporte de mercancías y optimización logística.

¿Es posible calcular la distancia entre dos puntos en un espacio n-dimensional? Sí, la fórmula de la distancia euclidiana se generaliza fácilmente a espacios n-dimensionales, donde la distancia entre dos puntos \((x_1, y_1, ..., z_1)\) y \((x_2, y_2, ..., z_2)\) es:

\[d(AB)=\sqrt{\sum_{i=1}^{n}(x_{2i} - x_{1i})^2}\]

¿Hay alguna diferencia entre la distancia y el desplazamiento en física y matemáticas? Sí, la distancia es la longitud total de la trayectoria recorrida, mientras que el desplazamiento es un vector que representa la distancia y la dirección desde el punto de inicio hasta el punto final, independientemente de la trayectoria.

¿Qué implica una distancia negativa o cero entre dos puntos en un contexto matemático o físico? En términos matemáticos, una distancia negativa no tiene significado, ya que la distancia siempre es no negativa. Una distancia de cero indica que los puntos son idénticos o que simplemente coinciden.

Distancia entre dos puntos: Aplicaciones

Distancia entre dos puntos en el plano cartesiano: En geometría, una aplicación fundamental del cálculo de la distancia entre dos puntos es en el plano cartesiano. La fórmula de la distancia entre dos puntos se utiliza para encontrar la longitud del segmento de línea que conecta dos puntos en un sistema de coordenadas cartesianas. Esto es esencial para calcular longitudes, áreas y volúmenes en figuras geométricas.

Resolución de problemas de distancia y velocidad: En álgebra, la distancia entre dos puntos se usa para resolver problemas relacionados con la velocidad, el tiempo y la distancia. Por ejemplo, si sabes la velocidad y el tiempo en que un objeto se mueve, puedes usar la fórmula de distancia entre dos puntos para calcular la distancia total recorrida. Además, en problemas de ecuaciones lineales, las coordenadas de dos puntos pueden representar dos puntos de una línea, y encontrar la distancia entre ellos puede ser útil para determinar la pendiente de la línea.

Distancia y desplazamiento en espacios tridimensionales: En cálculo vectorial, la distancia entre dos puntos se extiende al espacio tridimensional. Esta aplicación es fundamental en física y en la representación de trayectorias en 3D. Por ejemplo, en física, puedes calcular la distancia entre dos ubicaciones en el espacio tridimensional para determinar el trabajo realizado por una fuerza o la energía cinética. Además, en el diseño 3D y la animación, la distancia entre puntos se usa para crear trayectorias suaves para objetos en movimiento.

Estas aplicaciones en matemáticas demuestran cómo el cálculo de la distancia entre dos puntos es una herramienta esencial para resolver problemas geométricos, algebraicos y vectoriales en una variedad de contextos.