La circunferencia
Una circunferencia es el lugar geométrico de todos los puntos de un plano que equidistan de un punto fijo llamado centro.
Equidistar: Que se encuentran a la misma distancia. Los puntos de una circunferencia equidistan de su centro. Esta distancia se le denomina radio de la circunferencia y se denota por la letra \(r\).

Ecuación de la circunferencia con centro en el origen
Para hallar la ecuación de la circunferencia con centro en el origen, supongamos que tenemos una circunferencia de radio \(r\) tal que \(r>0\). Además, consideremos que el centro de esta circunferencia se encuentra en el origen de coordenadas del plano cartesiano, como se muestra en la siguiente figura.
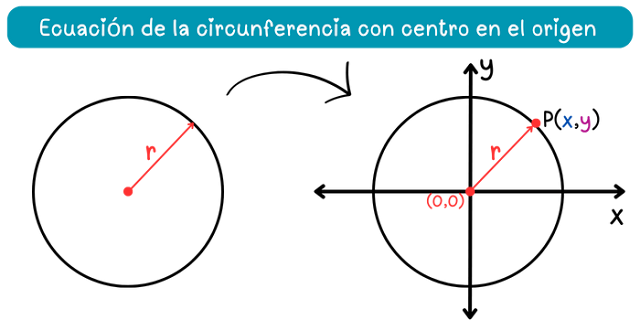
Con la circunferencia en el plano cartesiano, todos los puntos de la misma pueden representarse mediante coordenadas \((x, y)\) de la forma \(P(x, y)\). De acuerdo con la definición de la circunferencia, todos estos puntos se encuentran a una misma distancia \(r\) del origen. Por lo tanto, podemos establecer una relación algebraica entre los puntos de la circunferencia y el origen de coordenadas a través de su distancia, es decir, a través de \(r\).
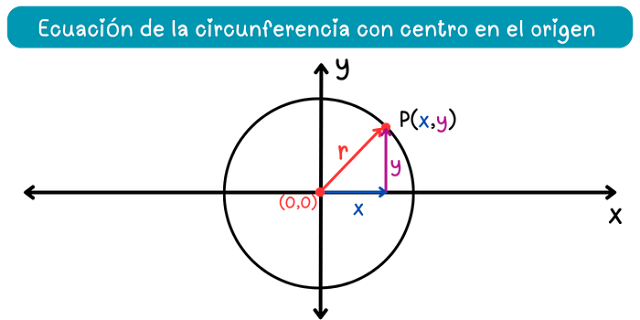
Observa que, en la figura, la coordenada \(x\) del punto \(P\) corresponde a la longitud de la base del triángulo rectángulo, mientras que la coordenada \(y\) corresponde a la longitud de la altura. Además, el radio de la circunferencia corresponde a la longitud de la hipotenusa. Al aplicar el teorema de Pitágoras, se obtiene:
Esta es la ecuación de la circunferencia con centro en el origen, donde \(r\) representa el radio y \((x, y)\) representa cualquier punto \(P\) perteneciente a la circunferencia.
Ecuación de la circunferencia con centro fuera del origen
Para hallar la ecuación de la circunferencia con centro fuera del origen, supongamos que en este caso, el centro de la circunferencia se encuentra fuera del origen de coordenadas del plano cartesiano, de manera que las coordenadas del centro sean \((h, k)\), como se muestra en la siguiente figura.
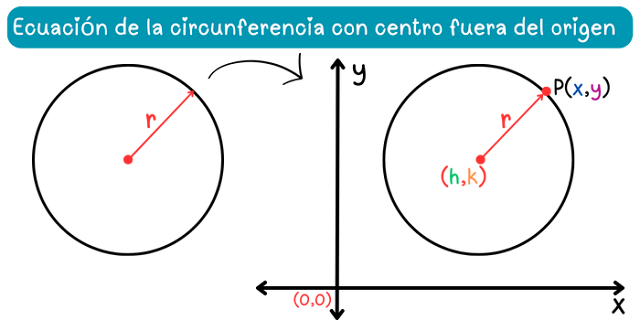
Podemos establecer una relación algebraica entre los puntos de la circunferencia y el centro de la circunferencia a través de su distancia, es decir, a través del radio \(r\).
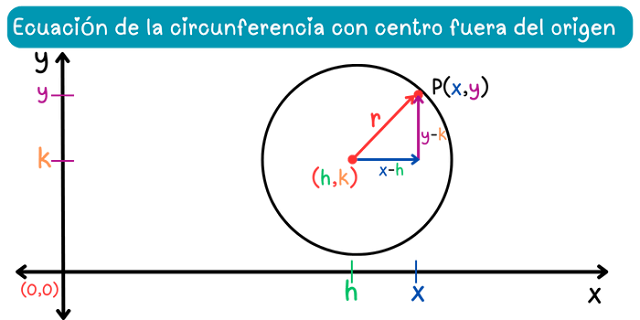
La longitud de la base del triángulo rectángulo está definida como \(x-h\) y la longitud de la altura como \(y-k\). Además, el radio \(r\) de la circunferencia corresponde a la longitud de la hipotenusa. Al aplicar el teorema de Pitágoras, se obtiene la siguiente ecuación:
Esta es la ecuación de la circunferencia con centro fuera del origen, en donde \(r\) es el radio, \((x, y)\) es cualquier punto \(P\) de la circunferencia y \((h,k)\) son las coordenadas del centro de la circunferencia. A la ecuación de la circunferencia con centro fuera del origen también se le conoce como ecuación ordinaria de la circunferencia.
Ecuación general de la circunferencia
La ecuación general de la circunferencia se obtiene simplemente al expandir los binomios al cuadrado de la ecuación de la circunferencia con centro fuera del origen. Al expandir los binomios al cuadrado de la ecuación de la circunferencia con centro fuera del origen, obtenemos:
De tal manera que, la ecuación de la circunferencia con centro fuera del origen se puede escribir como:
Ordenando los términos e igualando a cero esta ecuación obtenemos:
Para simplificar un poco esta ecuación realizamos los siguientes cambios de variable: \[\begin{aligned}A&=-2h\\B&=-2k\\C&=h^2+k^2-r^2\end{aligned}\] De tal manera que obtenemos la siguiente ecuación:
Esta es la ecuación general de la circunferencia o ecuación de la circunferencia en su forma general.
Para obtener el centro y radio de la circunferencia a partir de la ecuación general de la circunferencia, simplemente debemos realizar un despeje a los cambios de variable que hicimos anteriormente. Es decir, de los cambios de variable: \[\begin{aligned}A&=-2h\\B&=-2k\\C&=h^2+k^2-r^2\end{aligned}\] Obtenemos que:
Por lo tanto, el centro de la circunferencia en su forma general es:
El radio de la circunferencia en su forma general es:
A la ecuación general de la circunferencia también se le conoce como ecuación de la circunferencia en su forma general.
Ecuación de la circunferencia con centro en el origen ejercicios resueltos
Ejercicio 1. Hallar la ecuación de la circunferencia con centro en el origen de una circunferencia cuyo radio es \(r=8\).
Solución: Recuerda que la ecuación de la circunferencia con centro en el origen está dada por: \[x^2+y^2=r^2\] Si el radio es \(r=8\), la ecuación es simplemente: \[\begin{aligned}x^2+y^2&=8^2\\x^2+y^2&=64\end{aligned}\]
Ejercicio 2. Hallar la ecuación de la circunferencia que pasa por el punto \((2, 5)\).
Solución: Primero, notemos que la única información proporcionada en el enunciado es que la circunferencia pasa por un punto \(P\), por lo tanto, podemos asumir que la circunferencia está centrada en el origen de coordenadas. En este caso, su ecuación toma la forma estándar: \[x^2+y^2=r^2\] Para hallar el radio de esta circunferencia, simplemente sustituimos los valores de las coordenadas del punto \(P\), es decir: \[\begin{aligned}2^2+5^5&=r^2\\4+9&=r^2\\14&=r^2\\\sqrt{14}&=\sqrt{r^2}\\\sqrt{14}&=r\end{aligned}\] Por lo tanto, la ecuación de la circunferencia que pasa por el punto \(P(2, 5)\) es: \[\begin{aligned}x^2+y^2&=\left(\sqrt{14}\right)^2\\x^2+y^2&=14\end{aligned}\]
Ejercicio 3. Determinar si el punto \(P(2, 6)\) pertenece a la circunferencia cuya ecuación es: \[x^2+y^2=40\]
Solución: Para determinar si un punto \(P\) pertenece a una circunferencia, simplemente debemos verificar que la coordenada del punto satisface la igualdad de la ecuación. Tenemos la ecuación de la circunferencia definida como: \[x^2+y^2=40\] Si sustituimos \(P(2, 6)\) obtenemos: \[\begin{aligned}x^2+y^2&=2^2+6^2\\&=4+36\\&=40\end{aligned}\] Como se satisface la igualdad, entonces \(P(2, 6)\) pertenece a la circunferencia de la ecuación dada.
Ejercicio 4: Si una circunferencia con centro en el origen tiene un radio de 7 unidades, ¿cuál es su ecuación?
Solución: Para encontrar la ecuación de una circunferencia con centro en el origen y un radio dado, podemos usar la forma general de la ecuación de una circunferencia: \[x^2+y^2=r^2\] Donde \(x\) y \(y\) son las coordenadas de un punto en la circunferencia y \(r\) es el radio de la circunferencia. En este caso, el radio dado es \(r=7\), entonces la ecuación de la circunferencia con centro en el origen y un radio de 7 unidades es: \[x^2+y^2=7^2\] Simplificando: \[x^2+y^2=49\] Esta es la ecuación de la circunferencia con centro en el origen y radio \(r=7\)
Ejercicio 5: Determina si el punto \((0, -2)\) se encuentra en el interior, en la circunferencia o fuera de la circunferencia cuyo centro está en el origen de coordenadas y tiene un radio \(r=4\).
Solución: Para determinar si el punto \((0, -2)\) se encuentra dentro, en la circunferencia o fuera de la circunferencia, debemos verificar que el punto dado satisface la ecuación de la circunferencia con centro en el origen y radio \(r=4\), es decir, que al sustituir las coordenadas del punto en la ecuación se obtenga una igualdad verdadera. La ecuación de la circunferencia con centro en el origen está definida como: \[x^2+y^2=r^2\] Para una circunferencia con centro en el origen y un radio \(r=4\) se tiene la siguiente ecuación: \[\begin{aligned}x^2+y^2&=4^2\\x^2+y^2&=16\end{aligned}\] Ahora, sustituyendo los valores del punto en la ecuación, obtenemos: \[\begin{aligned}x^2+y^2&=16\\(0)^2+(-2)^2&=16\\0+4&=16\\4&=16\end{aligned}\] Como la igualdad \(4=16\) claramente es falsa, entonces el punto (0, -2) no satisface la ecuación de la circunferencia con centro en el origen y radio 4. En otras palabras, el punto (0, -2) está fuera de la circunferencia.
Ejercicio 6: ¿Cuál es el radio de la circunferencia con centro en el origen que pasa por el punto \((6, 8)\)?
Solución: Para encontrar el radio de la circunferencia con centro en el origen que pasa por el punto \((6, 8)\), aplicamos directamente la ecuación de la circunferencia con centro en el origen definida como: \[x^2+y^2=r^2\] Donde \(x\) y \(y\) son las coordenadas del punto en cuestión, y \(r\) es el radio de la circunferencia. En este caso, la coordenada del punto dado es \((6, 8)\), y queremos encontrar el radio \(r\) de la circunferencia, para esto sustituimos los valores de la coordenada en la ecuación: \[\begin{aligned}x^2+y^2&=r^2\\6^2+8^2&=r^2\\36+64&=r^2\\100&=r^2\end{aligned}\] Para encontrar el valor de \(r\), simplemente tomamos la raíz cuadrada de ambos lados de la ecuación, es decir: \[\begin{aligned}100&=r^2\\\sqrt{100}&=\sqrt{r^2}\\10&=r\end{aligned}\] Por lo tanto, el radio de la circunferencia con centro en el origen que pasa por el punto \((6, 8)\) es \(r=10\).
Ecuación de la circunferencia con centro fuera del origen ejercicios resueltos
Ejercicio 7. Hallar la ecuación de una circunferencia con centro en \((4, 2)\) y radio \(r=3\).
Solución: Recuerda que la ecuación de la circunferencia con centro fuera del origen está dada por:Ejercicio 8: Hallar la ecuación de una circunferencia con centro en \((-1, -5)\) y radio \(r=3\).
Solución: Para hallar la ecuación de una circunferencia con centro fuera del origen, primero debes recordar que esta ecuación está definida como:Ecuación general de la circunferencia ejercicios resueltos
Ejercicio 12. Hallar la ecuación ordinaria y general de una circunferencia con centro en \((2, 5)\) y radio \(r=4\).
Solución: Recuerda que la ecuación ordinaria de una circunferencia con centro en \((h, k)\) y radio \(r\) está dada por:Ejercicio 13: Hallar la ecuación ordinaria y general de una circunferencia con centro en \((3, 4)\) y radio \(r=7\).
Solución: Para obtener la ecuación general de la circunferencia, simplemente debemos desarrollar los términos cuadráticos de la ecuación ordinaria de la circunferencia en cuestión. Por lo tanto, primero necesitamos hallar la ecuación ordinaria de la circunferencia. La ecuación ordinaria de la circunferencia (ecuación de la circunferencia con centro fuera del origen) está definida como: