La ecuación de la circunferencia con centro fuera del origen
La ecuación de la circunferencia con el centro fuera del origen, también conocida como ecuación ordinaria de la circunferencia, se define de la siguiente manera: \[(x-h)^2+(y-k)^2=r^2\]
Veamos cómo se obtiene esta ecuación, en qué consiste cada término y cómo aplicar dicha ecuación en la resolución de ejercicios.
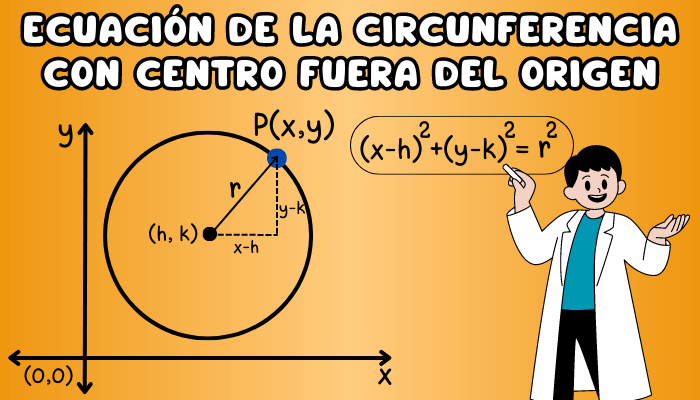
Deducción de la ecuación de la circunferencia con centro fuera del origen
Para encontrar la ecuación de la circunferencia con centro fuera del origen, utilizaremos el plano cartesiano y aplicaremos el teorema de Pitágoras.
Supongamos que tenemos una circunferencia de radio \(r\) tal que \(r>0\). Además, supongamos que colocamos el centro de esta circunferencia en algún punto del plano cartesiano, fuera del origen de coordenadas, tal como se muestra la siguiente figura.
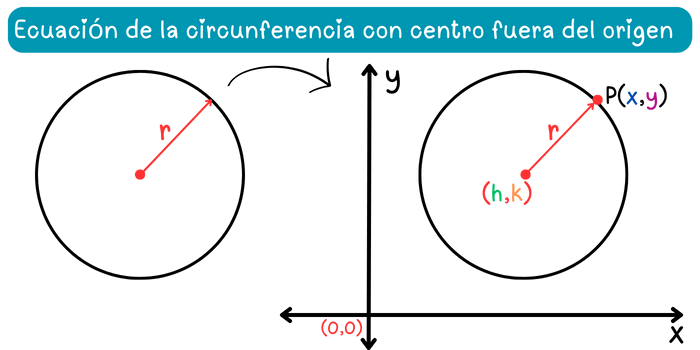
En el plano cartesiano, podemos asignar las coordenadas \((h, k)\) al centro de la circunferencia y representar todos los puntos de esta circunferencia mediante las coordenadas \((x, y)\). De acuerdo con la definición de circunferencia, todos los puntos se encuentran a una misma distancia \(r\) del centro. Por lo tanto, podemos establecer una relación algebraica entre los puntos de la circunferencia y el centro a través de la distancia \(r\) utilizando el teorema de Pitágoras.
El teorema de Pitágoras establece que, en un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, es decir: \[a^2+b^2=c^2\]
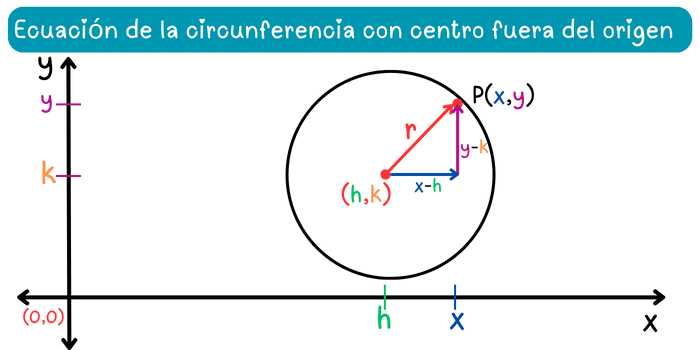
En la figura, la base del triángulo rectángulo se define como \(h-k\), y la altura se define como \(y-k\). Además, la hipotenusa del triángulo corresponde al radio \(r\) de la circunferencia. Aplicando el teorema de Pitágoras obtenemos la siguiente relación: \[(x-h)^2+(y-k)^2=r^2\] Esta es la ecuación de la circunferencia con centro fuera del origen, donde \(r\) es el radio, \((h, k)\) es la coordenada del centro y \((x, y)\) representa cualquier punto de la circunferencia.
Ecuación de la circunferencia con centro fuera del origen ejercicios resueltos
Ejercicio 1. Obtener el radio y centro de la circunferencia definida por la ecuación:\[(x-4)^2+(y-6)^2=9\]
Solución: La ecuación de la circunferencia con centro fuera del origen está dada por: \[(x-h)^2+(y-k)^2=r^2\] Donde \((h, k)\) es el centro y \(r\) es el radio de la circunferencia. Comparando esta ecuación con la del enunciado, obtenemos las siguientes relaciones: \[\begin{aligned}x-h&=x-4\\y-k&=y-6\\r^2&=9\end{aligned}\] De la primera igualdad despejamos \(h\): \[\begin{aligned}x-h&=x-4\\-h&=x-4-x\\-h&=-4\\h&=4\end{aligned}\] De la segunda igualdad despejamos \(k\): \[\begin{aligned}y-k&=y-6\\-k&=y-6-y\\-k&=-6\\k&=6\end{aligned}\] De la tercera igualdad despejamos \(r\) \[\begin{aligned}r^2&=9\\\sqrt{r^2}&=\sqrt{9}\\r&=3\end{aligned}\] Por lo tanto, concluimos que el radio de la circunferencia es \(r=3\) y el centro está en la coordenada \[(h,k)=(4, 6)\] La siguiente imagen muestra la gráfica de esta circunferencia en el plano cartesiano. Como podrás observar, la coordenada del centro está en la coordenada \((4, 6)\) y el radio de la circunferencia es \(r=3\).
Ejercicio 2. ¿Cuál es el centro y radio de la circunferencia definida por la siguiente ecuación?\[(x+3)^2+(y+5)^2=25\]
Solución: Recuerda que, la ecuación de la circunferencia con centro fuera del origen está definida como: \[(x-h)^2+(y-k)^2=r^2\] Donde \((h, k)\) es el centro y \(r\) es el radio de la circunferencia. Comparando esta ecuación con la del enunciado obtenemos las siguientes relaciones: \[\begin{aligned}x-h&=x+3\\y-k&=y+5\\r^2&=25\end{aligned}\] De la primera igualdad despejamos \(h\): \[\begin{aligned}x-h&=x+3\\-h&=x+3-x\\-h&=3\\h&=-3\end{aligned}\] De la segunda igualdad despejamos \(k\): \[\begin{aligned}y-k&=y+5\\-k&=y+5-y\\-k&=5\\k&=-5\end{aligned}\] De la tercera igualdad despejamos \(r\): \[\begin{aligned}r^2&=25\\\sqrt{r^2}&=\sqrt{25}\\r&=5\end{aligned}\] Concluimos que el centro de la circunferencia está en la coordenada \((-3, -5)\) y el radio es \(r=5\).
Ejercicio 3: Hallar el centro y radio de la circunferencia definida por la siguiente ecuación: \[(x+5)^2+(y-2)^2=16\]
Solución: Observa que la ecuación dada corresponde a la ecuación de una circunferencia con centro fuera del origen cuya estructura es: \[(x-h)^2+(y-k)^2=r^2\] Donde \((h, k)\) corresponde al centro de la circunferencia y \(r\) a la magnitud del radio. Comparando ambas ecuaciones se obtienen las siguientes relaciones: \[\begin{aligned}x-h&=x+5\\y-k&=y-2\\r^2&=16\end{aligned}\] De la primera igualdad despejamos \(h\): \[\begin{aligned}x-h&=x+5\\-h&=x+5-x\\-h&=5\\h&=-5\end{aligned}\] De la segunda igualdad despejamos \(k\): \[\begin{aligned}y-k&=y-2\\-k&=y-2-y\\-k&=-2\\k&=2\end{aligned}\] De esta manera encontramos que el centro de la circunferencia es: \[(h, k)=(-5, 2)\] Por último, de la tercera igualdad despejamos \(r\) para hallar el radio de la circunferencia: \[\begin{aligned}r^2&=16\\\sqrt{r^2}&=\sqrt{16}\\r&=4\end{aligned}\] Así concluimos que la circunferencia tiene un radio \(r=4\).
Ejercicio 4: Obtener el centro y radio de la circunferencia a partir de la ecuación ordinaria \[(x-7)^2+(y+9)^2=8\]
Solución: Para hallar el centro y radio de la circunferencia debemos comparar la ecuación dada con la ecuación ordinaria (ecuación de la circunferencia con centro fuera del origen) definida por: \[(x-h)^2+(y-k)^2=r^2\] Donde \((h, k)\) indican la coordenada del centro de la circunferencia y \(r\) representa la longitud del radio. Comparando ambas ecuaciones obtenemos las siguientes relaciones: \[\begin{aligned}x-h&=x-7\\y-k&=y+9\\r&=8\end{aligned}\] Para obtener el centro de la circunferencia \((h, k\) debemos despejar \(h\) de la primera igualdad y \(k\) de la segunda igualdad, es decir: \[\begin{aligned}x-h&=x-7\\-h&=x-7-x\\-h&=-7\\h&=7\\y-k&=y+9\\-k&=y+9-y\\-k&=9\\k&=-9\end{aligned}\] Por lo tanto, las coordenadas del centro de la circunferencia son: \[(h, k)=(7, -9)\] Para obtener el radio de la circunferencia simplemente debemos despejar \(r\) de la tercera igualdad, es decir: \[\begin{aligned}r^2&=8\\\sqrt{r^2}&=\sqrt{8}\\r&=\sqrt{8}\end{aligned}\] De esta manera encontramos que el radio de la circunferencia es: \[r=\sqrt{8}\]
Ejercicio 5. Obtener la ecuación de una circunferencia con centro en (3, 2) y radio r=5.
Solución: El enunciado del ejercicio nos indica que el centro de la circunferencia está en la coordenada \((3, 2)\) y su radio es \(r=5\), por lo que, simplemente debemos sustituir estos valores en la ecuación de la circunferencia con centro fuera del origen: \[(x-h)^2+(y-k)^2=r^2\] Donde \((h, k)\) corresponde al centro de la circunferencia y \(r\) al radio. Sustituyendo los datos del enunciado, obtenemos: \[\begin{aligned}(x-3)^2+(y-2)^2&=5^2\\(x-3)^2+(y-2)^2&=25\end{aligned}\] Concluimos que, la ecuación de la circunferencia con centro en \((3, 2)\) y radio \(r=5\) es: \[(x-3)^2+(y-2)^2=25\]
Ejercicio 6. Obtener la ecuación de la circunferencia con centro en (-1, -5) y radio r=8.
Solución: Simplemente debemos sustituir los valores dados en la ecuación de la circunferencia con centro fuera del origen. Recuerda que esta ecuación está dada por: \[(x-h)^2+(y-k)^2=r^2\] Entonces, sustituyendo los valores obtenemos:
Por lo tanto, concluimos que la ecuación de la circunferencia con centro en \((-1, -5)\) y radio \(r=8\) es: \[(x+1)^2+(y+5)^2=64\]
Ejercicio 7. Obtener la ecuación de la circunferencia con centro en (-5, 3) y radio r=9.
Solución: Recuerda que la ecuación de la circunferencia con centro fuera del origen está definida por: \[(x-h)^2+(y-k)^2=r^2\] Donde \((h, k)\) es el centro y \(r\) es el radio. En este caso, el enunciado nos indica que el centro está en la coordenada \((-5, 3)\) y el radio es \(r=9\), por lo que, simplemente debemos reemplazar estos valores en la ecuación. Es decir: \[\begin{aligned}(x-h)^2+(y-k)^2&=r^2\\(x-(-5))^2+(y-3)^2&=9^2\\(x+5)^2+(y-3)^2&=81\end{aligned}\] De esta manera concluimos que la ecuación de la circunferencia con centro en \((-5, 3)\) y radio \(r=9\) es: \[(x+5)^2+(y-3)^2=81\]
Ejercicio 8: Calcular la ecuación ordinaria de una circunferencia con centro en (8, -1) y radio \(r=7\).
Solución: La ecuación ordinaria, también conocida como la ecuación de una circunferencia con centro fuera del origen, está dada de la siguiente manera: \[(x-h)^2+(y-k)^2=r^2\] En esta ecuación, los valores \(h\) y \(k\) representan las coordenadas del centro de la circunferencia, es decir, \((h, k)\), y \(r\) representa la longitud del radio. Para obtener la ecuación deseada, simplemente sustituimos los valores conocidos en la ecuación: \[\begin{aligned}(x-h)^2+(y-k)^2&=r^2\\(x-8)^2+(y-(-1))^2&=7^2\end{aligned}\] Simplificando: \[\begin{aligned}(x-8)^2+(y-(-1))^2&=7^2\\(x-8)^2+(y+1)^2&=49\end{aligned}\] Por lo tanto, la ecuación ordinaria de la circunferencia con centro en (8, -1) y radio \(r=7\) es: \[(x-8)^2+(y+1)^2=49\] Esta ecuación describe la circunferencia completa con precisión.
Ejercicio 9: Hallar la ecuación de la circunferencia con centro en (-1, -3) y que pasa por el punto (2, 5).
Solución: Observa que se nos pide hallar la ecuación de una circunferencia con centro fuera del origen. La ecuación de una circunferencia con centro en \((h, k)\) y radio \(r\) está dada por: \[(x - h)^2 + (y - k)^2 = r^2\] De acuerdo con la información del enunciado, la coordenada del centro de la circunferencia es \((-1, -3)\) y queremos encontrar la ecuación de la circunferencia que pasa por el punto \((2, 5)\). Al conocer un punto por el que pasa la circunferencia, este nos ayudará a determinar el radio, ya que el radio es la distancia entre el centro \((-1, -3)\) y el punto \((2, 5)\). La distancia entre dos puntos se define como la longitud del segmento de recta que une los puntos. La fórmula para hallar la distancia entre dos puntos está definida por: \[d(A, B)=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\] Sustituyendo las coordenadas de los puntos, obtenemos: \[\begin{aligned}d(A, B)&=\sqrt{\left(x_{2}-x_{1}\right)^2+\left(y_{2}-y_{1}\right)^2}\\&=\sqrt{(2-(-1))^2+(5-(-3))^2}\\&=\sqrt{(2+1)^2+(5+3)^2}\\&=\sqrt{3^2+8^2}\\&=\sqrt{9+64}\\&=\sqrt{73}\end{aligned}\] Por lo tanto el radio de la circunferencia es \(r=\sqrt{73}\). Ahora que tenemos el valor de \(r\), podemos escribir la ecuación de la circunferencia, es decir: \[\begin{aligned}(x-h)^2+(y-k)^2&=r^2\\(x-(-1))^2+(y-(-3))^2&=\left(\sqrt{73}\right)^2\end{aligned}\] Simplificando obtenemos: \[\begin{aligned}(x-(-1))^2+(y-(-3))^2&=\left(\sqrt{73}\right)^2\\(x+1)^2+(y+3)^2&=73\end{aligned}\] Concluimos que esta es la ecuación de la circunferencia con centro en (-1, -3) y que pasa por el punto (2, 5).
Ejercicio 10: Dada la ecuación de una circunferencia \((x+3)^2+(y-2)^2=9\), determinar si los puntos (2, 3) y (-1, 4) están dentro de la circunferencia, en la circunferencia o fuera de ella.
Solución: Para determinar si los puntos (2, 3) y (-1, 4) están dentro, en la circunferencia o fuera de ella, primero debemos identificar todos los parámetros que describen la circunferencia en cuestión. Observa que la ecuación proporcionada en el enunciado corresponde a la ecuación de una circunferencia con centro fuera del origen, que sigue la estructura general: \[(x-h)^2+(y-k)^2=r^2\] Donde las coordenadas \((h, k)\) corresponden al centro de la circunferencia y \(r\) representa la magnitud del radio. En este caso, el centro es \((-3, 2)\) y el radio es \(r=3\). La clave para determinar la posición de los puntos dados con respecto a la circunferencia es calcular la distancia desde el centro a cada uno de ellos. Si la distancia es menor que el radio, el punto se encuentra dentro de la circunferencia; si la distancia es igual al radio, el punto está sobre la circunferencia, y si la distancia es mayor que el radio, el punto está fuera de la circunferencia. Para el punto (2, 3), usemos la ecuación de la circunferencia para calcular la distancia desde el centro \((-3, 2)\) hasta el punto (2, 3): \[\begin{aligned}d&=\sqrt{(2-(-3))^2+(3-2)^2}\\&=\sqrt{5^2+1^2}\\&=\sqrt{26}\end{aligned}\] Dado que \(\sqrt{26} > 3\), podemos concluir que el punto (2, 3) está fuera de la circunferencia. Para el punto (-1, 4), nuevamente empleamos la ecuación de la circunferencia para calcular la distancia desde el centro \((-3, 2)\) hasta el punto (-1, 4): \[\begin{aligned}d&=\sqrt{(-1-(-3))^2+(4-2)^2}\\&=\sqrt{2^2+2^2}\\&=\sqrt{8}\end{aligned}\] En este caso, \(\sqrt{8} > 3\), por lo que el punto (-1, 4) también se encuentra fuera de la circunferencia. En resumen, ambos puntos (2, 3) y (-1, 4) están ubicados fuera de la circunferencia proporcionada.
Ecuación de la circunferencia con centro fuera del origen ejercicios para practicar
Ejercicio 1. Dada la siguiente ecuación de la circunferencia, encuentra el centro \((h, k)\) y el radio \(r\) de la circunferencia. \[(x-h)^2 + (y-k)^2 = r^2\]
Ejercicio 2. Encuentra el centro y el radio de la circunferencia definida por la ecuación: \[(x+3)^2 + (y-4)^2 = 25\]
Ejercicio 3. Grafica la circunferencia con centro en \((2, -1)\) y radio \(r=4\).
Ejercicio 4. Dado un punto \(P(x_1, y_1)\) en el borde de la circunferencia y el centro \(C(h, k)\), encuentra la distancia desde \(P\) hasta \(C\), es decir, encuentra la longitud del segmento de recta \(PC\).
Ejercicio 5. Encuentra la ecuación de la recta tangente a la circunferencia definida por la siguiente ecuación en el punto \((3, 1)\). \[(x-1)^2 + (y+2)^2 = 9\]
Ejercicio 6. Si el centro de una circunferencia se mueve desde el punto \(P(1, 2)\) hasta el punto \(Q(5, -3)\), encuentra la ecuación de la circunferencia en cada posición.
Ejercicio 7. Supongamos que una antena de transmisión tiene una cobertura circular con centro en \((-2, 1)\) y un radio de \(10\) km. ¿Cuál es la ecuación de la cobertura?