La ecuación de la circunferencia con centro en el origen
La ecuación de la circunferencia con centro en el origen y radio \(r\) está definida como: \[x^2+y^2=r^2\]
Veamos cómo se obtiene esta ecuación y en qué consiste cada uno de sus términos.
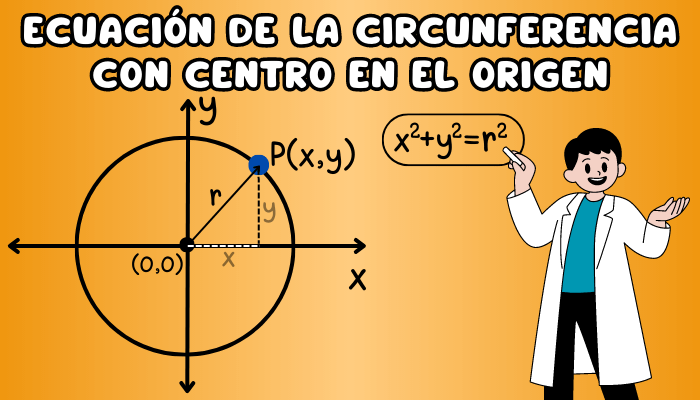
Deducción de la ecuación de la circunferencia con centro en el origen
Para encontrar la ecuación de una circunferencia con centro en el origen, utilizaremos el plano cartesiano y aplicaremos el teorema de Pitágoras.
Supongamos que tenemos una circunferencia de radio \(r\) donde \(r>0\). Ahora, coloquemos el centro de esta circunferencia en el origen de coordenadas del plano cartesiano, como se muestra en la siguiente figura.
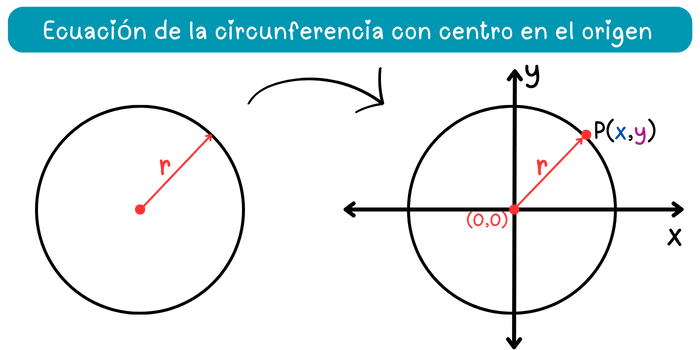
Ahora que la circunferencia está en el plano cartesiano, todos los puntos de esta circunferencia se pueden representar mediante coordenadas \((x, y)\). De acuerdo con la definición de circunferencia, todos estos puntos se encuentran a una misma distancia \(r\) del origen de coordenadas. Por lo tanto, podemos establecer una relación algebraica entre los puntos de la circunferencia y el origen de coordenadas utilizando el teorema de Pitágoras y la distancia \(r\). El teorema de Pitágoras establece que, en un triángulo rectángulo la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, es decir: \[a^2+b^2=c^2\]
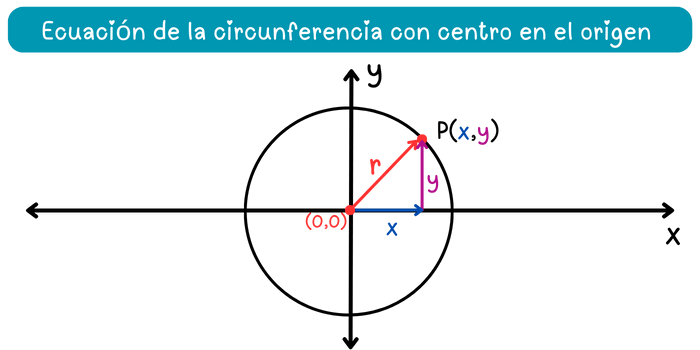
En la figura, la coordenada \(x\) del punto \(P\) corresponde a la longitud de la base del triángulo rectángulo, mientras que la coordenada \(y\) corresponde a la longitud de la altura. Además, el radio \(r\) de la circunferencia corresponde a la longitud de la hipotenusa. Aplicando el teorema de Pitágoras se obtiene: \[x^2+y^2=r^2\] Esta es la ecuación de la circunferencia con centro en el origen, donde \(r\) es el radio y \((x, y)\) es cualquier punto de la circunferencia.
Ecuación de la circunferencia con centro en el origen ejercicios resueltos
Ejercicio 1. Determinar la ecuación de la circunferencia con centro en el origen y de radio \(r=10\).
Solución: La ecuación de una circunferencia con centro en el origen está definida como: \[x^2+y^2=r^2\] Dado que la circunferencia tiene un radio \(r=10\), la ecuación que la describe es: \[\begin{aligned}x^2+y^2&=10^2\\x^2+y^2&=100\end{aligned}\] Esta es la ecuación de la circunferencia con centro en el origen y radio \(r=10\).
Ejercicio 2. Determinar la ecuación de una circunferencia centrada en el origen y radio \(r=3/4\).
Solución: Recuerda que la ecuación de una circunferencia con centro en el origen está definida como: \[x^2+y^2=r^2\] Como el radio de la circunferencia es \(r=\frac{3}{4}\), entonces su ecuación es: \[\begin{aligned}x^2+y^2&=\left(\frac{3}{4}\right)^2\\x^2+y^2&=\frac{9}{16}\end{aligned}\]
Ejercicio 3. Obtener el radio de la circunferencia definida por la siguiente ecuación: \[x^2+y^2=9\]
Solución: La ecuación de la circunferencia con centro el origen es: \[x^2+y^2=r^2\] En este ejercicio, debemos determinar el radio de la circunferencia descrita por la ecuación: \[x^2+y^2=9\] Para hacerlo, vamos a comparar estas dos ecuaciones y encontrar el valor de \(r\). La igualdad que debemos cumplir es \(r^2=9\), para hallar el valor de \(r\) aplicamos raíz cuadrada en ambos miembros de la igualdad: \[\begin{aligned}r^2&=9\\\sqrt{r^2}&=\sqrt{9}\\r&=3\end{aligned}\] Por lo tanto, el radio de la circunferencia es \(r=3\)
Ejercicio 4. Obtener el radio de la circunferencia definida por la ecuación: \[x^2+y^2=\sqrt{9}\]
Solución: Nuevamente, la ecuación de la circunferencia con centro en el origen está dada por: \[x^2+y^2=r^2\] Debemos hallar el radio de una circunferencia cuya ecuación es: \[x^2+y^2=\sqrt{9}\] Observa que esta ecuación se puede simplicar al hallar la raíz cuadrada, es decir: \[\begin{aligned}x^2+y^2&=\sqrt{9}\\x^2+y^2&=3\end{aligned}\] Por lo tanto, debe cumplirse que \(r^2=3\). Para hallar el valor de \(r\) aplicamos raíz cuadrada en ambos miembros de la igualdad: \[\begin{aligned}r^2&=3\\\sqrt{r^2}&=\sqrt{3}\\r&=\sqrt{3}\end{aligned}\] Por lo tanto, el radio de la circunferencia es \(r=\sqrt{3}\)
Ejercicio 5. Obtener la ecuación de la circunferencia con centro en el origen cuyo radio es \(r=5\).
Solución: Sabemos que la ecuación de la circunferencia con centro en el origen está dada por: \[x^2+y^2=r^2\] Por lo tanto, sustituyendo el valor de \(r=5\) en la ecuación, obtenemos que: \[\begin{aligned}x^2+y^2&=5^2\\x^2+y^2&=25\end{aligned}\] En conclusión, la ecuación de la circunferencia con centro en el origen de radio \(r=5\) es: \[x^2+y^2=25\]
Ejercicio 6. Encuentra la ecuación de la circunferencia con centro en el origen y que pasa por el punto \(P(3, 4)\).
Solución: Recuerda que, en la ecuación de la circunferencia con centro en el origen, \(r\) es el radio y \(P(x, y)\) es cualquier punto de la circunferencia, por lo tanto, conociendo el punto \(P(3, 4)\), podemos obtener el radio de la circunferencia simplemente sustituyendo estos valores en la ecuación, es decir: \[\begin{aligned}x^2+y^2&=r^2\\3^2+4^2&=r^2\\9+16&=r^2\\25&=r^2\\\sqrt{25}&=\sqrt{r^2}\\5&=r\end{aligned}\] De tal manera que la ecuación de la circunferencia que pasa por el punto \(P(3, 4)\) es: \[x^2+y^2=5^2\]
Ejercicio 7. Determinar si el punto \(P(5, 6)\) pertenece a la circunferencia cuya ecuación está definida como: \[x^2+y^2=61\]
Solución: Para determinar si un punto pertenece a una circunferencia, simplemente debemos probar que este cumple la ecuación, es decir, que al sustituir los valores del punto la igualdad sea verdadera: \[\begin{aligned}x^2+y^2&=r^2\\5^2+6^2&=61\\61&=61\end{aligned}\] Como la igualdad es verdadera, entonces el punto \(P(5, 6)\) pertenece a la circunferencia cuya ecuación es \(x^2+y^2=61\)
Ejercicio 8. Determina si el punto \((7, 8)\) está en la circunferencia descrita por la ecuación \[x^2+y^2=94\]
Solución. Para determinar si un punto pertenece a una circunferencia, debemos comprobar que al sustituir las coordenadas del punto en la ecuación se satisfaga la igualdad. Sustituyendo los valores \(x=7\) y \(y=8\) obtenemos: \[\begin{aligned}x^2+y^2&=94\\7^2+8^2&=94\\49+64&=96\\113&\neq 96\end{aligned}\] Como 113 no es igual a 94, entonces la ecuación no es verdadera. Esto significa que el punto (7, 8) no es parte de la circunferencia dada.
Ecuación de la circunferencia con centro en el origen ejercicios
Determina la ecuación de la circunferencia con centro en el origen y radio 12.
Solución: La ecuación de la circunferencia con centro en el origen es: \(x^2+y^2=r^2\). Por lo tanto, si la circunferencia tiene un radio \(r=12\), entonces su ecuación se obtiene simplemente al sustituir el valor del radio en la ecuación, es decir: \[\begin{aligned}x^2+y^2&=r^2\\x^2+y^2&=12^2\\x^2+y^2&=144\end{aligned}\] De esta manera, \(x^2+y^2=144\) es la ecuación de una circunferencia de radio \(r=12\) centrada en el origen.
¿Cuál es la ecuación de la circunferencia con centro en el origen y radio de 4 unidades?
Respuesta: La ecuación de la circunferencia con centro en el origen se expresa como: \(x^2+y^2=r^2\). Si la circunferencia tiene un radio \(r\) de 4 unidades, para obtener su ecuación simplemente debemos sustituir el valor de \(r\) en la ecuación anterior, es decir: \[\begin{aligned}x^2+y^2&=r^2\\x^2+y^2&=4^2\\x^2+y^2&=16\end{aligned}\] De esta manera, obtenemos que la ecuación de una circunferencia con centro en el origen y radio de 4 unidades es: \[x^2+y^2=16\]
¿Cuál es la ecuación de una circunferencia con centro en el origen y radio igual a 3?
Respuesta: La ecuación de una circunferencia de radio \(r\) con centro en el origen está dada por: \[x^2+y^2=r^2\] Si la circunferencia tiene un radio \(r\) igual a 3, entonces su ecuación se obtiene sustituyendo este valor en la ecuación anterior, es decir: \[\begin{aligned}x^2+y^2&=r^2\\x^2+y^2&=3^2\\x^2+y^2&=9\end{aligned}\] Por lo tanto, la ecuación de una circunferencia con centro en el origen y radio igual a 3 es: \[x^2+y^2=9\]
¿Cuál es la ecuación de una circunferencia con radio de 7 unidades?
Respuesta: Según la información proporcionada en la pregunta, estamos tratando con una circunferencia que tiene su centro en el origen. Si la circunferencia tiene un radio \(r\) de 7 unidades, podemos determinar su ecuación al sustituir el valor de \(r\) en la ecuación estándar de una circunferencia con centro en el origen, que es la siguiente: \[x^2+y^2=r^2\] Sustituyendo el valor del radio \(r=7\), obtenemos: \[\begin{aligned}x^2+y^2&=r^2\\x^2+y^2&=7^2\\x^2+y^2&=49\end{aligned}\] Por lo tanto, la ecuación de una circunferencia con centro en el origen y radio \(r=7\) es: \[x^2+y^2=49\]
Ecuación de la circunferencia con centro en el origen ejercicios para practicar
Ejercicio 1. Determina la ecuación de una circunferencia con centro en el origen y radio 5.
Ejercicio 2. Dada la ecuación de una circunferencia: \(x^2+y^2=9\), ¿cuál es el radio de la circunferencia?
Ejercicio 3. Encuentra el radio de la circunferencia cuya ecuación es: \[x^2+y^2=25\]
Ejercicio 4. Determina la ecuación de la circunferencia con centro en el origen que pasa por el punto (3, 4).
Ejercicio 5. Determina si el punto (6, 8) se encuentra dentro o fuera de la circunferencia con centro en el origen y radio 7.
Ejercicio 6. Encuentra la distancia entre el centro de la circunferencia (0, 0) y el punto (3, 4) que está sobre la circunferencia.
Ejercicio 7. Escribe la ecuación de la circunferencia con centro en el origen y que pase por el punto (-2, -2).
Ejercicio 8. Determina si los puntos (1, 1) y (3, 3) están en la misma circunferencia con centro en el origen.
Ejercicio 9. Encuentra la ecuación de una circunferencia con centro en el origen que sea tangente al eje x en el punto (5, 0).
Ejercicio 10. Encuentra la ecuación de una circunferencia con centro en el origen que sea tangente al eje y en el punto (0, -4).
Ecuación de la circunferencia con centro en el origen preguntas frecuentes
¿Qué es la ecuación de la circunferencia con centro en el origen? La ecuación de la circunferencia con centro en el origen es una expresión algebraica que describe todos los puntos en un plano que están a una misma distancia r del origen de coordenadas (0, 0). Se representa como: \[x^2+y^2=r^2\]
¿Cómo se interpreta la ecuación \(x^2+y^2=r^2\)? La ecuación \(x^2+y^2=r^2\) significa que cada punto \((x, y)\) que satisfaga esta ecuación estará exactamente a una distancia \(r\) del origen \((0, 0)\). Los valores \(x\) y \(y\) son las coordenadas de algún punto, y \(r\) es el radio de la circunferencia.
¿Cómo encuentro el radio de la circunferencia si tengo su ecuación con centro en el origen? En la ecuación \(x^2+y^2=r^2\), el valor de \(r\) es el radio de la circunferencia. Si la ecuación está en esta forma estándar, simplemente toma la raíz cuadrada positiva de \(r^2\) para obtener el valor del radio.
¿Cómo determino si un punto está en la circunferencia con centro en el origen? Para determinar si un punto \((x, y)\) está en la circunferencia con centro en el origen, simplemente sustituye los valores \(x\) y \(y\) en la ecuación \(x^2+y^2=r^2\). Si la ecuación es verdadera, el punto está en la circunferencia; si es falsa, el punto no está en la circunferencia.
¿Cómo relaciono la ecuación de la circunferencia con el Teorema de Pitágoras? La ecuación de la circunferencia \(x^2+y^2=r^2\) está relacionada con el Teorema de Pitágoras. Si consideras un punto \((x, y)\) en la circunferencia, las coordenadas \(x\) y \(y\) son las longitudes de los catetos de un triángulo rectángulo. Aplicando el Teorema de Pitágoras, obtendrás \(x^2 + y^2 = r^2\).
¿Cómo encuentro las coordenadas del centro de la circunferencia si tengo su ecuación? En la ecuación \(x^2+y^2=r^2\), el centro de la circunferencia está en el origen \((0, 0)\). Por lo tanto, las coordenadas del centro son \(x = 0\) y \(y = 0\).
¿Qué ocurre si el valor de \(r\) en la ecuación \(x^2+y^2=r^2\) es negativo? En la ecuación de la circunferencia, el radio \(r\) debe ser un valor positivo, ya que se refiere siempre a la distancia desde el centro de la circunferencia hasta cualquier punto en la circunferencia. Un valor negativo no tendría sentido en este contexto.
¿Qué relación hay entre la ecuación \(x^2+y^2=r^2\) y la fórmula general de la ecuación de la circunferencia? La ecuación \(x^2+y^2=r^2\) es la forma específica de la ecuación de la circunferencia con centro en el origen. La fórmula general de la ecuación de la circunferencia es \((x - h)^2 + (y - k)^2 = r^2\), donde \((h, k)\) son las coordenadas del centro.
¿Qué sucede si el valor de \(r\) en la ecuación \(x^2+y^2=r^2\) es cero? Si \(r=0\), la ecuación se convierte en \(x^2+y^2=0\). Esto implica que \(x=0\) y \(y=0\), lo que significa que se tiene un punto de coordenadas \((0, 0)\). En otras palabras, una circunferencia centrada al origen con radio \(r=0\) es simplemente un punto en el origen de coordenadas.
¿Cómo afecta el cambio de \(r\) a la posición y el tamaño de la circunferencia? A medida que el valor de \(r\) aumenta, la circunferencia se expande y cuando \(r\) disminuye, la circunferencia se contrae. El centro permanece en el origen en ambos casos.