¿Qué es el teorema de Pitágoras y por qué es importante?
El teorema de Pitágoras es una de las fórmulas matemáticas más conocidas y utilizadas en todo el mundo. Su importancia y aplicación se extienden a múltiples campos, desde la arquitectura hasta la física y la astronomía. Pero ¿sabes realmente en qué consiste este teorema y cómo se aplica en la resolución de problemas cotidianos? Si quieres descubrir todo lo que necesitas saber sobre el teorema de Pitágoras, has llegado al lugar indicado. En esta entrada te explicamos de manera clara y detallada qué es el teorema de Pitágoras, cómo se aplica en situaciones cotidianas y cómo se han desarrollado diferentes demostraciones y variaciones a lo largo de la historia. ¡No te pierdas esta oportunidad de descubrir uno de los teoremas matemáticos más fascinantes y útiles de todos los tiempos!

Teorema de Pitágoras
Para cuando tenemos un triángulo rectángulo, es decir, un triángulo en el que uno de sus ángulos mide 90°, existe un teorema que relaciona las longitudes de los tres lados, este es el teorema de Pitágoras, que nos dice que:En un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Si en un triángulo rectángulo las longitudes de los catetos son \(a\) y \(b\), y la longitud de la hipotenusa es \(c\), entonces el teorema de Pitágoras se traduce a: \[\begin{aligned}a^2+b^2=c^2\end{aligned}\]
Catetos e hipotenusa del triángulo rectángulo
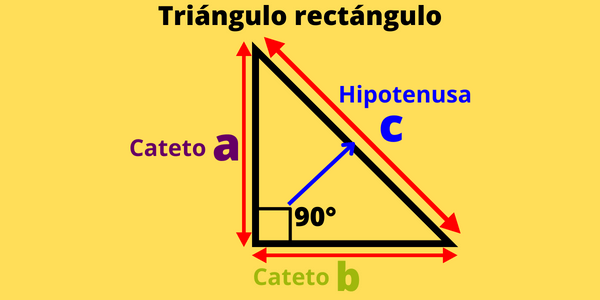
En un triángulo rectángulo los catetos son los lados que forman el ángulo recto. En la siguiente figura son los lados de longitud \(a\) y \(b\). La hipotenusa es el lado opuesto al ángulo recto, en la figura es el lado de longitud \(c\). También puedes identificar a la hipotenusa como el lado de mayor longitud del triángulo rectángulo.
Ecuaciones del teorema de Pitágoras
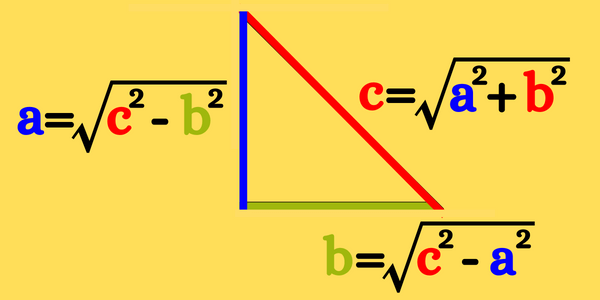
La ecuación que representa el teorema de Pitágoras es una ecuación de tres términos algebraicos: \(a^2\), \(b^2\) y \(c^2\). Para hallar el valor numérico de uno de estos términos es necesario conocer los otros dos, por ejemplo: Si conocemos la longitud de los catetos \(a\) y \(b\), entonces podemos hallar la longitud de la hipotenusa \(c\) simplemente despejando \(c\) de la ecuación principal, es decir: \[\begin{aligned}a^2+b^2&=c^2\\\sqrt{a^2+b^2}&=\sqrt{c^2}\\\sqrt{a^2+b^2}&=c\end{aligned}\] Si conocemos la longitud del cateto \(a\) y la longitud de la hipotenusa \(c\), entonces podemos hallar la longitud del cateto \(b\) simplemente despejando \(b\) de la ecuación principal, es decir: \[\begin{aligned}a^2+b^2&=c^2\\b^2&=c^2-a^2\\ \sqrt{b^2}&=\sqrt{c^2-a^2}\\b&=\sqrt{c^2-a^2}\end{aligned}\] Si conocemos la longitud del cateto \(b\) y la longitud de la hipotenusa \(c\), entonces podemos hallar la longitud del cateto \(a\) simplemente despejando \(a\) de la ecuación principal, es decir: \[\begin{aligned}a^2+b^2&=c^2\\a^2&=c^2-b^2\\ \sqrt{a^2}&=\sqrt{c^2-b^2}\\a&=\sqrt{c^2-b^2}\end{aligned}\] La siguiente imagen muestra la relación de las ecuaciones del teorema de Pitágoras con los lados del triángulo rectángulo
Teorema de Pitágoras - Ejercicios resueltos
Solución: Primero un consejo. Dibuja un triángulo rectángulo y coloca en él la información proporcionada por el enunciado del problema. Esto te ayudará a tener una idea general de lo que tienes y de lo que estás buscando.
Ahora bien, quizás te preguntes, ¿A cuál de los dos catetos se le asigna el valor de 5 m y cuál el valor de 10 m? Recuerda que los catetos son los dos lados que forman el ángulo recto del triángulo rectángulo, pero no importa a cuál de los dos le asignes primero un valor, el resultado siempre será el mismo. Se puede ver esto con más claridad al desarrollar la solución de este ejemplo. La siguiente imagen muestra cómo hemos asignado los valores a los catetos:
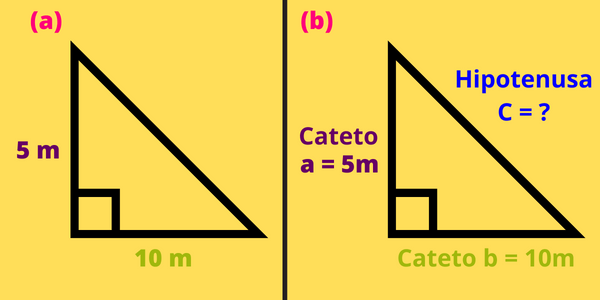
La ecuación para hallar la longitud de la hipotenusa, conociendo las longitudes de los catetos \(a\) y \(b\) es: \[c=\sqrt{a^2+b^2}\] Sustituyendo los valores de \(a=5m\) y \(b=10m\) obtenemos que: \[\begin{aligned}c&=\sqrt{(5m)^2+(10m)^2}\\&=\sqrt{25m^2+100m^2}\\&=\sqrt{125m^2}\\&=11.18m\end{aligned}\] Por lo tanto, la longitud de la hipotenusa es \(c=11.18m\)
La siguiente imagen muestra un arreglo en el que ha cambiado el orden de asignación de las longitudes de los catetos, hagamos los cálculos para mostrar que el orden de asignación de los catetos es irrelevante, pues el resultado será el mismo.
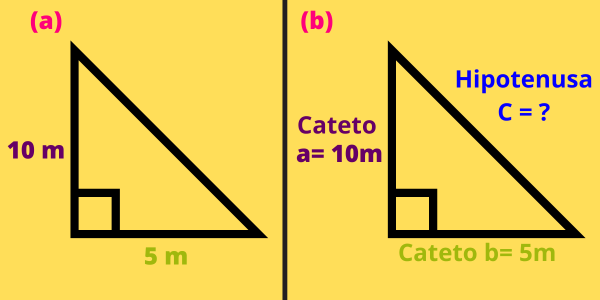
La ecuación para hallar la longitud de la hipotenusa, conociendo las longitudes de los catetos \(a\) y \(b\), sigue siendo: \[c=\sqrt{a^2+b^2}\] Sustituyendo los valores de \(a=10m\) y \(b=5m\) obtenemos que: \[\begin{aligned}c&=\sqrt{(10m)^2+(5m)^2}\\&=\sqrt{100m^2+25m^2}\\&=\sqrt{125m^2}\\&=11.18m\end{aligned}\] Cómo podrás observar el resultado en ambos casos es el mismo.
Solución:
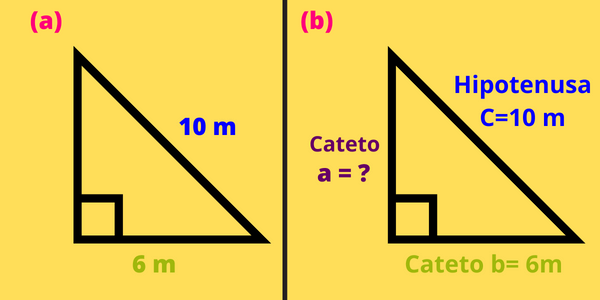
La ecuación para hallar la longitud del cateto \(a\), conociendo la longitud del cateto \(b\) y la longitud de la hipotenusa \(c\) es: \[a=\sqrt{c^2-b^2}\] Sustituyendo los valores de \(b=6m\) y \(c=10m\) obtenemos que: \[\begin{aligned}a&=\sqrt{(10m)^2-(6m)^2}\\&=\sqrt{100m^2-36m^2}\\&=\sqrt{64m^2}\\&=8 m\end{aligned}\] Por lo tanto, la longitud del cateto \(a\) es \(a=8m\)
Solución:
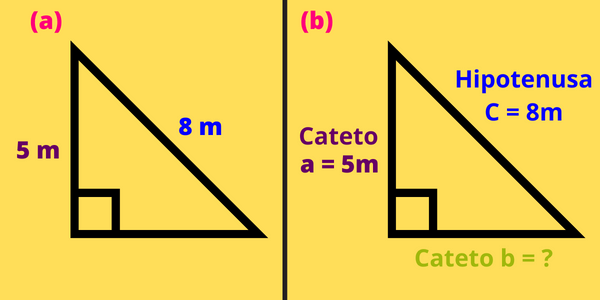
La ecuación para hallar la longitud del cateto \(b\), conociendo la longitud del cateto \(a\) y la longitud de la hipotenusa \(c\) es: \[b=\sqrt{c^2-a^2}\] Sustituyendo los valores de \(a=5m\) y \(c=8m\) obtenemos que: \[\begin{aligned}b&=\sqrt{(8m)^2-(5m)^2}\\&=\sqrt{64m^2-25m^2}\\&=\sqrt{39m^2}\\&=6.24 m\end{aligned}\] Por lo tanto, la longitud del cateto \(b\) es \(b=6.24m\)
¿El teorema de Pitágoras sólo se aplica a triángulos rectángulos?
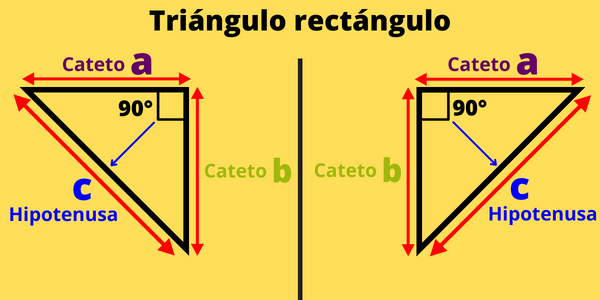
Si. Muchas veces la orientación del triángulo rectángulo puede confundir al momento de identificar los catetos y la hipotenusa de un triángulo, sin embargo, lo que debes recordar es que los catetos son los lados que forman el ángulo recto y la hipotenusa es el lado opuesto al ángulo recto. Las siguientes imágenes muestran cómo identificar estos elementos para diferentes orientaciones de un triángulo rectángulo.
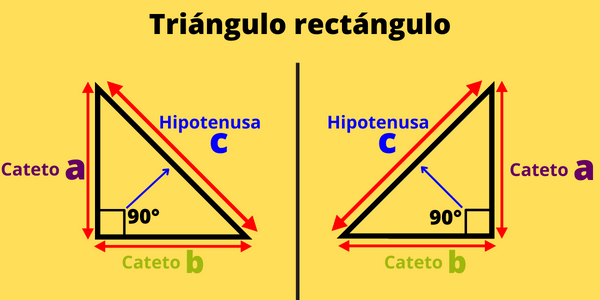
Independientemente de la orientación del triángulo rectángulo, los catetos serán siempre los lados que forman en ángulo recto (ángulo de 90°) y la hipotenusa siempre será el lado opuesto al ángulo recto.
Preguntas frecuentes sobre el teorema de Pitágoras
¿Qué es el Teorema de Pitágoras? El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados, conocidos como catetos. En términos algebraicos, se expresa como \(c^2 = a^2 + b^2\), donde \(c\) es la hipotenusa y \(a\) y \(b\) son los catetos.
¿Quién fue Pitágoras y por qué es importante su teorema? Pitágoras fue un matemático y filósofo griego, fundador de la escuela pitagórica en el siglo VI a.C. Su teorema es importante porque es uno de los pilares de la geometría y la trigonometría. Su escuela demostró y formalizó el teorema, sentando las bases para la comprensión de las relaciones entre los lados de un triángulo rectángulo.
¿Cómo se formula el Teorema de Pitágoras? El Teorema de Pitágoras se formula como \(c^2 = a^2 + b^2\), donde \(c\) es la longitud de la hipotenusa y \(a\) y \(b\) son las longitudes de los catetos en un triángulo rectángulo.
¿Cuál es la relación entre el Teorema de Pitágoras y los triángulos rectángulos? El Teorema de Pitágoras se aplica exclusivamente a los triángulos rectángulos, que son aquellos con un ángulo recto (90 grados). Este teorema establece una relación crucial entre las longitudes de sus lados.
¿Cómo se puede usar el Teorema de Pitágoras para encontrar una longitud desconocida? Si se conocen las longitudes de dos lados en un triángulo rectángulo, se puede usar el teorema para encontrar la longitud del tercer lado. Si se conoce la longitud de la hipotenusa y un cateto, se puede calcular el otro cateto mediante la fórmula \(a^2 = c^2 - b^2\) o \(b^2 = c^2 - a^2\).
¿Cuál es el uso práctico del Teorema de Pitágoras? El Teorema de Pitágoras tiene aplicaciones prácticas en muchas áreas. Se utiliza en arquitectura y construcción para verificar ángulos rectos y medir distancias diagonales. En navegación, ayuda a calcular distancias y ubicaciones en mapas. Además, en ciencias como la física y la ingeniería, se aplica en cálculos de fuerzas y distancias.
¿Cómo se demuestra el Teorema de Pitágoras? Hay diversas demostraciones del Teorema de Pitágoras, que van desde argumentos geométricos hasta pruebas algebraicas. Una demostración geométrica popular implica dividir un cuadrado grande en triángulos y cuadrados más pequeños y luego reorganizarlos para demostrar la igualdad de áreas.
¿Existen generalizaciones del Teorema de Pitágoras? Sí, existen generalizaciones para triángulos en otras geometrías y para espacios más allá de la geometría euclidiana. Además, el teorema se extiende a otras áreas matemáticas, como la teoría de números y la geometría tridimensional.
¿El Teorema de Pitágoras es válido en sistemas no euclidianos? El Teorema de Pitágoras es específico de la geometría euclidiana y no se mantiene en todas las geometrías. En geometrías no euclidianas, como la hiperbólica o la elíptica, el teorema puede no ser válido o puede requerir modificaciones.
¿Cómo influyó el Teorema de Pitágoras en el desarrollo de las matemáticas y la ciencia? El Teorema de Pitágoras tuvo un impacto profundo en el desarrollo de las matemáticas y la ciencia. Marcó el inicio de la demostración formal en matemáticas y sentó las bases para la geometría y la trigonometría. Su influencia se extiende hasta la actualidad, siendo esencial en campos como la física, la ingeniería y la astronomía.