Gráfica de una función
Si \(f\) es una función, entonces la gráfica de \(f\) es la representación de todos los pares ordenados \((x, f(x))\) de la función en el plano cartesiano. Los valores de la variable independiente \(x\) corresponden a todos los valores del dominio de la función y los valores \(f(x)\) corresponden a los valores asociados a la función (variable independiente).
¿Cómo graficar una función?
Para realizar la gráfica de una función es necesario conocer el dominio y rango de la función. La forma más sencilla de realizar la gráfica de una función es a través de una tabla de valores de dos columnas. En la columna izquierda de la tabla se coloca la variable independiente \(x\) y en la columna derecha se coloca el valor asociado a la variable, es decir, \(f(x)\) o \(y\).
Los valores que se le asignan a la variable independiente \(x\) en la primera columna son algunos valores que pertenecen al dominio de la función. En la columna derecha se colocan los valores que se obtienen al evaluar esta variable en la función \(f(x)\). Para obtener una idea general de la gráfica de la función, resulta una buena idea asignar a la variable independiente \(x\) valores negativos, positivos y el cero, siempre y cuando estos valores pertenezcan al dominio de la función.
El objetivo de realizar la tabla de dos columnas es poder asociar los valores de la tabla con puntos en el plano cartesiano, puntos de la forma \((x,f(x))\), donde los valores de \(x\) corresponden a los valores del eje \(x\) del plano cartesiano y los valores \(f(x)\) corresponden a puntos del eje \(y\) del plano cartesiano.

Gráfica de una función lineal
Solución: El dominio y rango de una función lineal corresponde al conjunto de los números reales, ya que al evaluar cualesquier número real en la función, la función no se indetermina. En este caso, a la variable independiente \(x\) le asignaremos los siguientes valores: \[\left\lbrace -3, -2, -1, 0, 1, 2 , 3\right\rbrace\] Evaluando cada uno de estos valores en la función, obtenemos la siguiente tabla.
| \(x\) | \(f(x)\) |
| \(-3\) | \(f(-3)=2\cdot(-3)=-6\) |
| \(-2\) | \(f(-2)=2\cdot(-2)=-4\) |
| \(-1\) | \(f(-1)=2\cdot(-1)=-2\) |
| \(0\) | \(f(0)=2\cdot(0)=0\) |
| \(1\) | \(f(1)=2\cdot1=2\) |
| \(2\) | \(f(2)=2\cdot2=4\) |
| \(3\) | \(f(3)=2\cdot3=6\) |
Como cada fila de la tabla es de la forma \((x, f(x))\), podemos ubicar estas coordenadas en el plano cartesiano para obtener una gráfica de puntos de la función.

Observa que, entre más valores de \(x\) se evalúan en la función \(f(x)\), más información se tendrá de la gráfica real de la función, sin embargo, la clave es simplemente unir los puntos que tenemos para tener una aproximación visual de la gráfica de la función. La siguiente imagen representa la gráfica de la función \(f(x)=2x\)
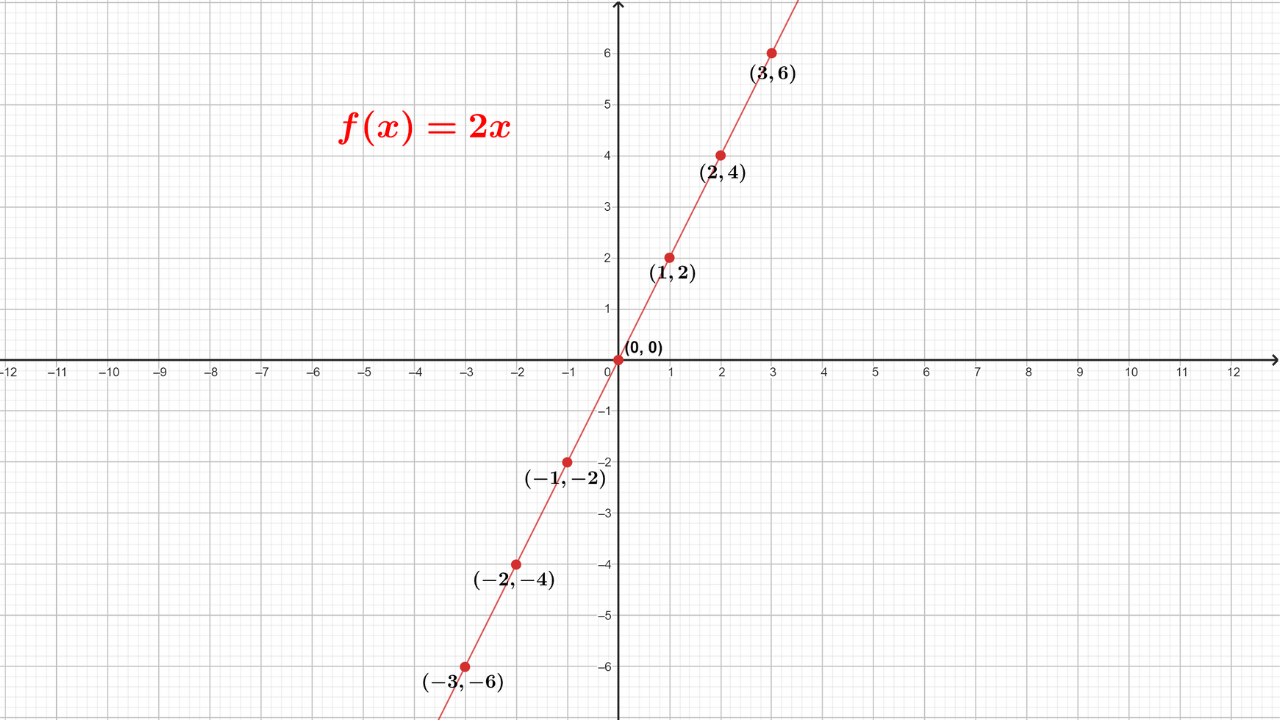
Nota. La gráfica de una función lineal es siempre una línea recta en un sistema de coordenadas cartesianas.
Características de la función lineal
Si \(A\) y \(B\) son conjuntos no vacíos, se define la función lineal como \(f:\mathbb{A}\rightarrow\mathbb{B}\), tal que para todo \(x\in A\) se cumple que: \[f(x)=mx+b\] La gráfica de una función lineal en el plano cartesiano es una línea recta. La pendiente de la recta es \(m\), y \(b\) es la ordenada al origen.
- Si \(m>0\) la función es creciente.
- Si \(m<0\) la función es decreciente.
Gráfica de una función cuadrática
Solución: El dominio de una función cuadrática es el conjunto de todos los números reales, ya que al evaluar cualesquier número real en la función, la función no se indetermina. En este caso, a la variable independiente \(x\) le asignaremos los siguientes valores: \[\left\lbrace-5, -3, -1, 0, 1, 3, 5\right\rbrace\]
| \(x\) | \(f(x)\) |
| \(-5\) | \(f(-5)=(-5)^2=25\) |
| \(-3\) | \(f(-3)=(-3)^2=9\) |
| \(-1\) | \(f(-1)=(-1)^2=1\) |
| \(0\) | \(f(0)=(0)^2=0\) |
| \(1\) | \(f(1)=(1)^2=1\) |
| \(3\) | \(f(3)=(3)^2=9\) |
| \(5\) | \(f(5)=(5)^2=25\) |
La idea de construir la tabla de valores es ver que cada fila es de la forma \((x, f(x))\). Graficando estas coordenadas en el plano cartesiano obtenemos la gráfica de puntos de la función.
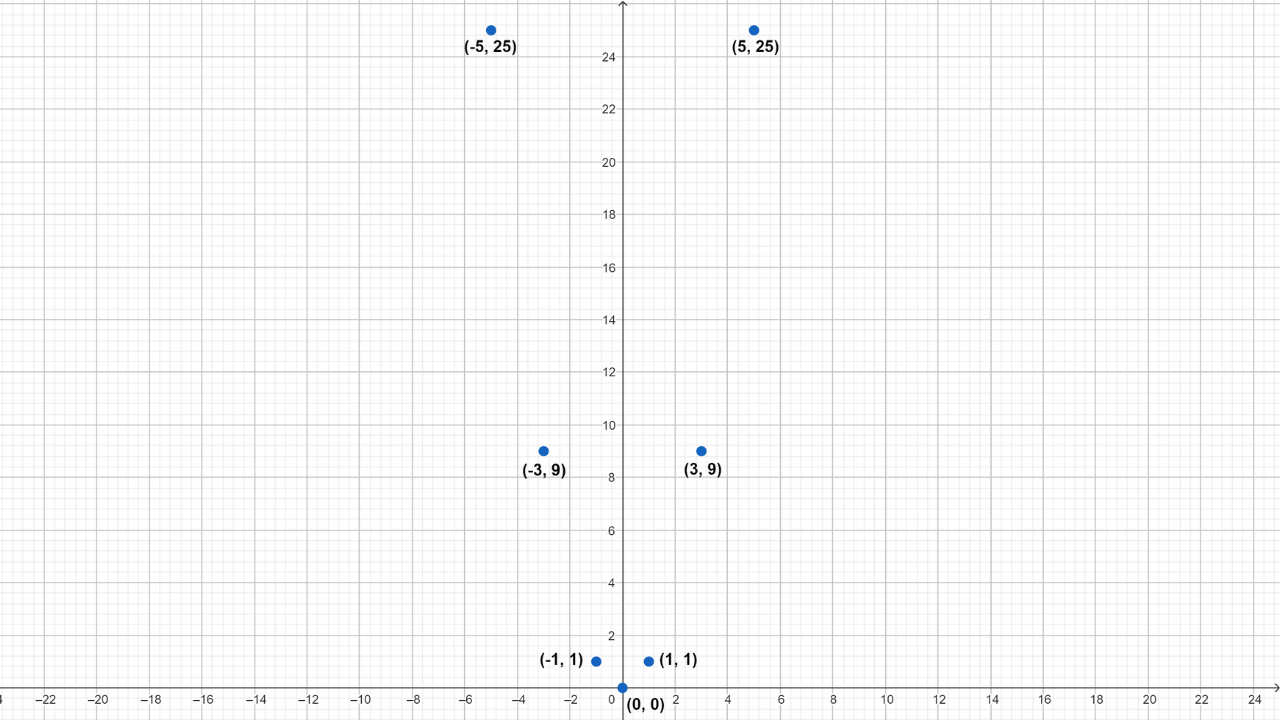
Observa que, si evaluamos más valores en la función \(f(x)\), más información tendremos de la gráfica real de la función, sin embargo, recuerda que la clave de este método es simplemente el de unir los puntos para tener una aproximación visual de la gráfica de la función. La siguiente imagen representa la gráfica de la función \(f(x)=x^2\)
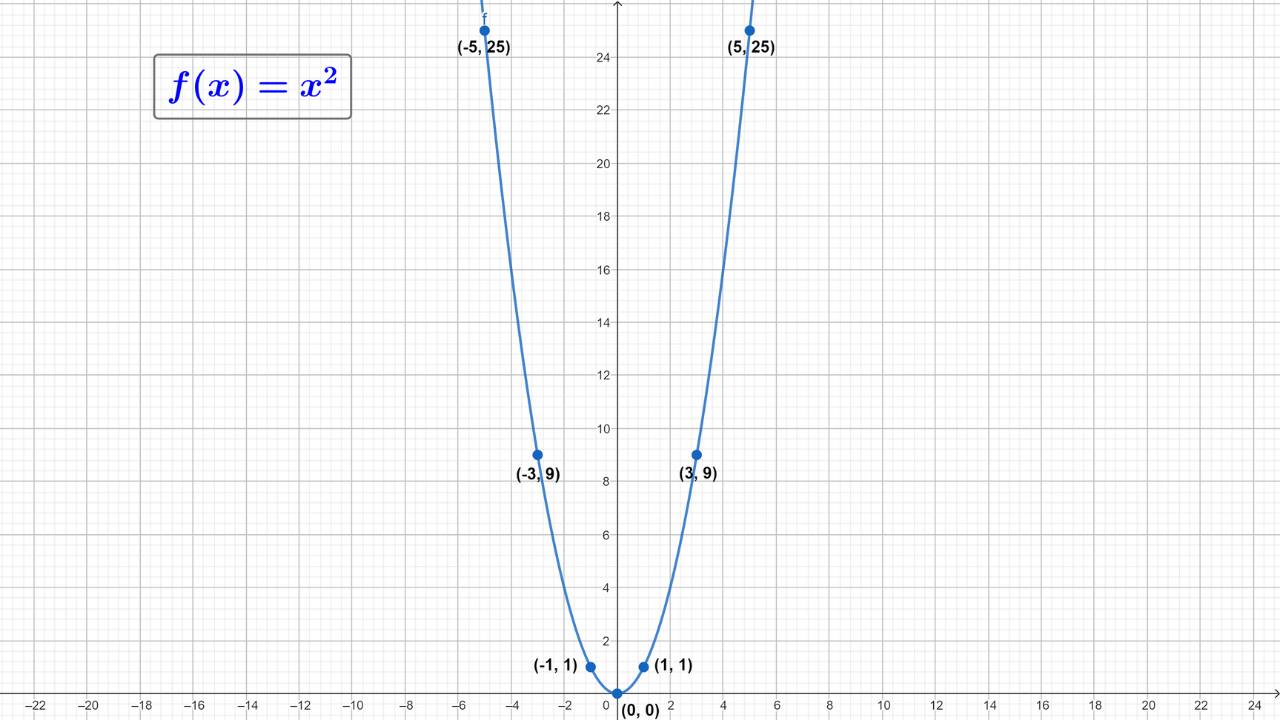
La gráfica de una función cuadrática corresponde a una parábola (curva con forma de “U”). La orientación de la parábola depende de la estructura de la función.
Características de la función cuadrática
Si \(A\) y \(B\) son conjuntos no vacíos, se define la función cuadrática como \(f:\mathbb{A}\rightarrow\mathbb{B}\), tal que para todo \(x\in A\) se cumple que: \[f(x)=ax^2+bx+c\] con \(a\neq 0\)
La gráfica de una función cuadrática en el plano cartesiano es una parábola. De acuerdo con la estructura de la función, el valor de la constante \(a\) representa la orientación y la amplitud de la función.
- Si \(a>0\) la gráfica estará abierta hacia arriba (forma de \(\cup\))
- Si \(a<0\) la gráfica estará abierta hacia abajo (forma de \(\cap\))
La apertura de la parábola depende del valor absoluto de \(a\), si \(|a|\) es un valor muy grande, entonces la gráfica crece (o decrece) más rápidamente y la apertura de la gráfica es muy cerrada, en caso contrario la gráfica crece (o decrece) más lentamente y la apertura de la gráfica es más abierta.
El vértice de la parábola representa un valor máximo o mínimo de la función, este valor depende de la orientación de la parábola, si \(a>0\) la función tendrá un valor mínimo y si \(a<0\) la función tendrá un valor máximo.La coordenada del vértice en el eje \(x\) es \(x=-\frac{b}{2a}\) y en el eje \(y\) es \(f\left(-\frac{b}{2a}\right)\)
Los puntos de intersección de la función con el eje \(x\) están dados por \[x_{1,2}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
Gráfica de la función raíz cuadrada
Solución: El dominio de la función raíz cuadrada consta de todos los valores de \(x\) para los que el radicando (expresión dentro del radical) no es negativo. Esto debido a que, al trabajar con números reales únicamente podemos calcular la raíz cuadrada de los números positivos y del cero. En este caso, le asignaremos a la variable independiente \(x\) los siguientes valores: \[\left\lbrace0, 1, 2, 3, 4, 5, 6, 7\right\rbrace\] Evaluando cada uno de estos valores en la función, obtenemos la siguiente tabla:
| \(x\) | \(f(x)\) |
| \(0\) | \(f(0)=\sqrt{0}=0\) |
| \(1\) | \(f(1)=\sqrt{1}=1\) |
| \(2\) | \(f(2)=\sqrt{2}=1.41\) |
| \(3\) | \(f(3)=\sqrt{3}=1.73\) |
| \(4\) | \(f(4)=\sqrt{4}=2\) |
| \(5\) | \(f(5)=\sqrt{5}=2.23\) |
| \(6\) | \(f(6)=\sqrt{6}=2.44\) |
| \(7\) | \(f(7)=\sqrt{7}=2.64\) |
Al ser cada fila de la tabla de la forma \((x, f(x))\), podemos ubicar estas coordenadas en el plano cartesiano para obtener la gráfica de puntos de la función.
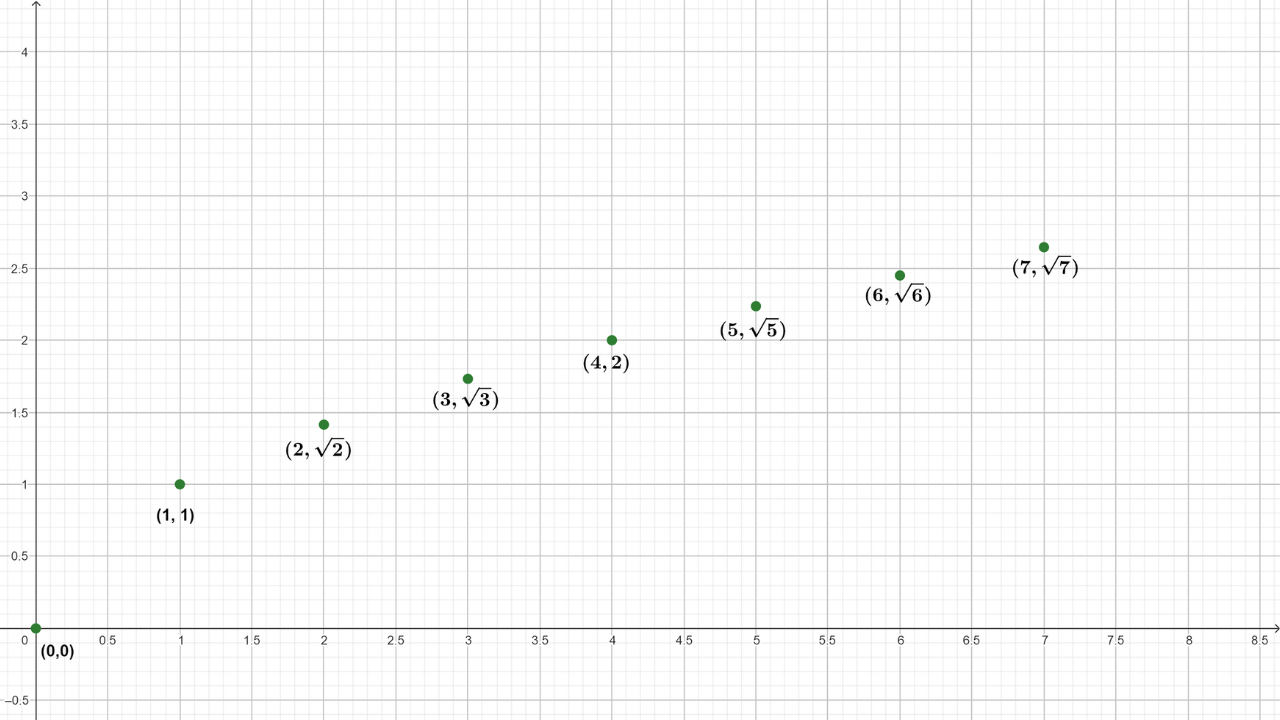
Observa que entre más valores de \(x\) se evalúen en la función \(f(x)\) más información se tendrá de la gráfica real de la función, sin embargo, la clave es simplemente unir los puntos que tenemos para tener una aproximación visual de la gráfica de la función. La siguiente imagen representa la gráfica de la función \(f(x)=\sqrt{x}\)
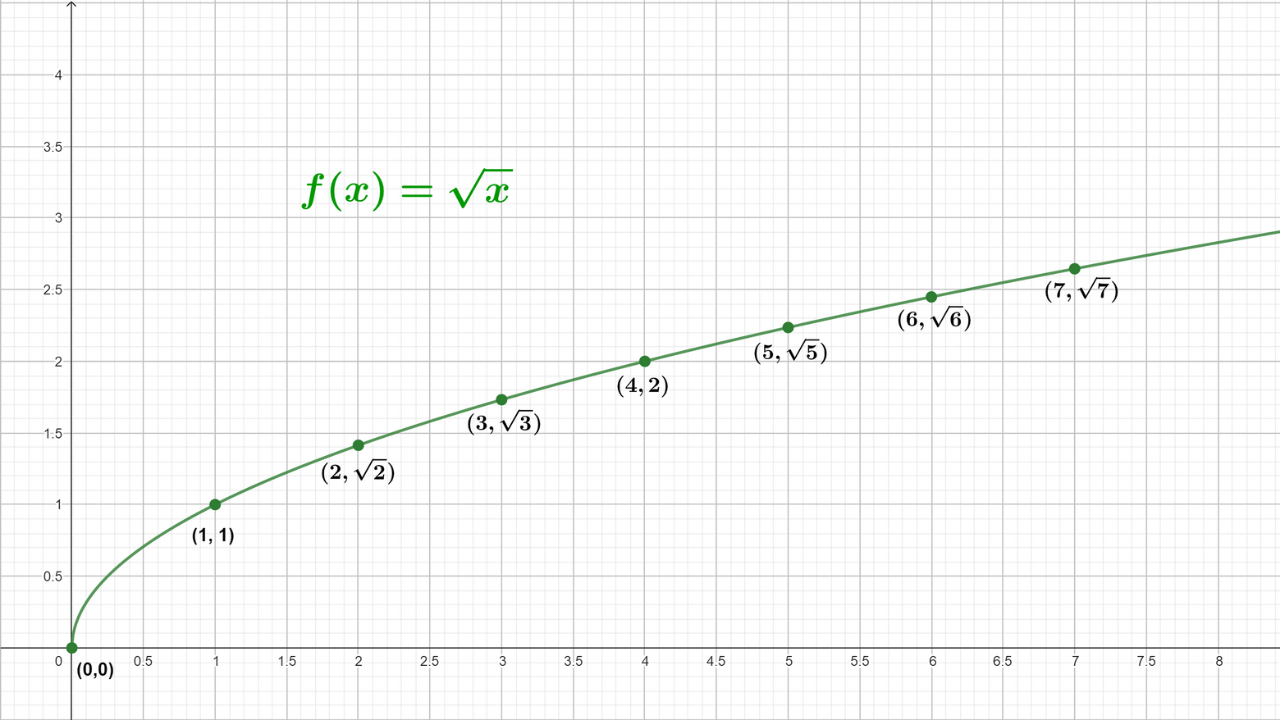
La gráfica de la función raíz cuadrada corresponde a la mitad de una parábola como las que conocemos de la función cuadrática, el eje de simetría de la media parábola es una recta horizontal (paralela al eje \(y\))
Características de la función raíz cuadrada
Si \(A\) y \(B\) son conjuntos no vacios, se define la función raíz cuadrada como \(f:\mathbb{A}\rightarrow\mathbb{B}\), tal que para todo \(x\in A\) se cumple que: \[f(x)=\sqrt{x}\]
Los valores de \(x\in A\) deben cumplir que \(x\geq 0\), esto debido a que en los números reales la raíz cuadrada sólo está definida para números positivos y para el cero. La gráfica de la función raíz cuadrada en el plano cartesiano es la mitad de una parábola.