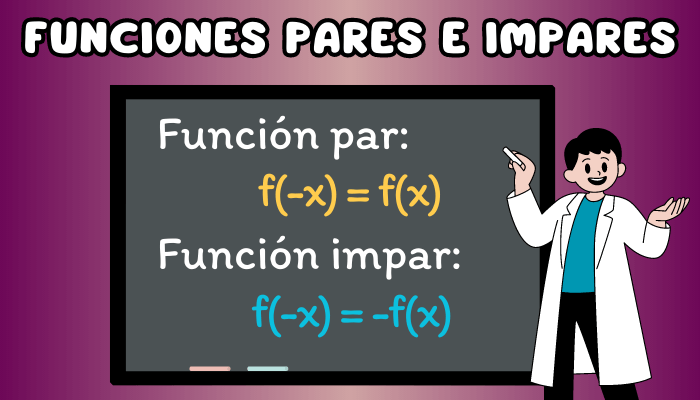
Funciones pares e impares
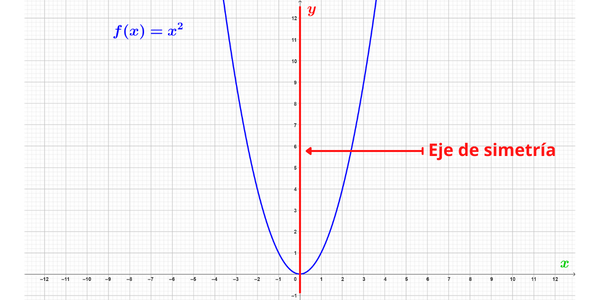
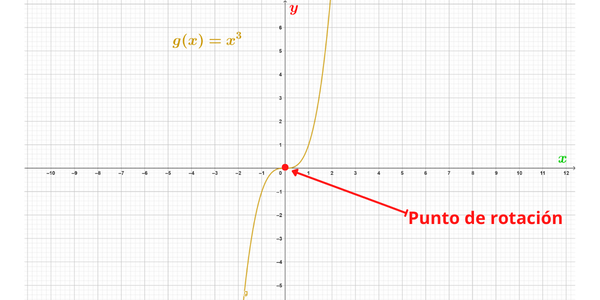
Una función es par, si para cada valor de \(x\) en el dominio de \(f\) se cumple que:\[f(-x)=f(x)\] La gráfica de una función par es simétrica con respecto al eje \(y\). Una función es impar, si para cada valor de \(x\) en el dominio de \(f\) se cumple que:\[f(-x)=-f(x)\] La gráfica de una función impar presenta simetría rotacional con respecto al origen de coordenadas, es decir, la gráfica de la función no cambia si se rota 180°. A continuación, te presentamos la gráfica de una función par y una función impar en el plano cartesiano.
Función par ejemplo
Función impar ejemplo
¿Cómo determinar si una función es par o impar?
El método para determinar si una función es par, impar o ninguna de las dos, consiste en aplicar directamente la definición. Observa que la definición de función par y función impar involucran una igualdad, en la que para ambos casos el primer miembro es \(f(-x)\), esta es la clave, ya que simplemente debemos sustituir \(-x\) en la función en la que queremos determinar si es par o impar y si obtenemos que \(f(-x)\) es igual a \(f(x)\), entonces \(f\) será una función par, pero si \(f(-x)\) es igual a \(-f(x)\), entonces \(f\) será una función impar. Si \(f(-x)\) no es igual a ninguna de estas dos, entonces \(f\) no será una función par ni impar. A continuación, te presentamos una serie de ejemplos que te ayudará a comprender a cómo determinar la paridad de una función.
Funciones pares e impares ejemplos

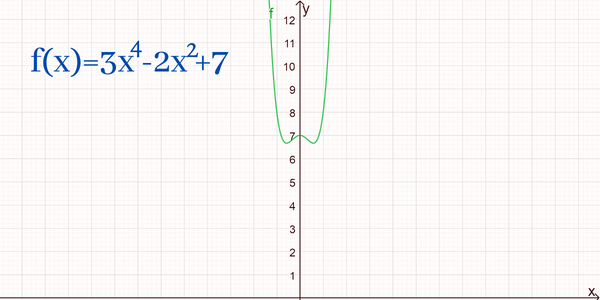

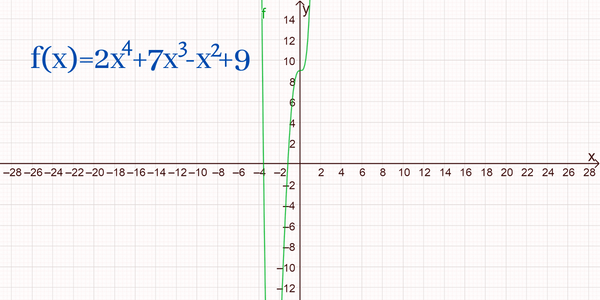
¿Existe una función que sea par e impar al mismo tiempo?
Si. La única función que es par e impar al mismo tiempo, es la función nula. Demostración. Sea \(f\) una función cualesquiera. Supongamos que esta función es par, es decir: \[f(-x)=f(x)\] Además, supongamos que esta función también es impar, es decir: \[f(-x)=-f(x)\] Como hablamos de la misma función \(f\), entonces se cumple que: \[f(-x)=f(-x)\] A partir de esta igualdad obtenemos que: \[\begin{aligned}f(x)&=-f(x)\\f(x)+f(x)&=0\\2f(x)&=0\\f(x)&=0\end{aligned}\] Por lo tanto, la única función que es par e impar al mismo tiempo es la función nula \(f(x)=0\).
Propiedades de las funciones pares e impares: Demostración
La función constante es par
Propiedad 1. La función constante es par. Es decir, \[f(x)=k=f(-x)\] Demostración. Sea \(f\) la función constante definida por: \(f(x)=k\). Como \(f(x)=k\) para toda \(x\), entonces: \[\begin{aligned}f(-x)=k=f(x)\end{aligned}\]
La suma de funciones pares es par
Propiedad 2. La suma de funciones pares es una función par. Es decir, \[(f+g)(-x)=(f+g)(x)\] Demostración. Sean \(f\) y \(g\) dos funciones pares, es decir: \[\begin{aligned}f(-x)&=f(x)\\g(-x)&=g(x)\end{aligned}\] De acuerdo con el álgebra de funciones: \((f+g)(x)=f(x)+g(x)\), entonces: \[\begin{aligned}(f+g)(-x)&=f(-x)+g(-x)\\&=f(x)+g(x)\\&=(f+g)(x)\end{aligned}\]
La suma de funciones impares es impar
Propiedad 3. La suma de funciones impares es impar. Es decir: \[(f+g)(-x)=-(f+g)(x)\] Demostración. Sean \(f\) y \(g\) dos funciones impares, es decir: \[\begin{aligned}f(-x)&=-f(x)\\g(-x)&=-g(x)\end{aligned}\] Entonces:\[\begin{aligned}(f+g)(-x)&=f(-x)+g(-x)\\&=-f(x)+(-g(x))\\&=-f(x)-g(x)\\&=-(f(x)+g(x))\\&=-(f+g)(x)\end{aligned}\]
El producto de dos funciones pares es par
Propiedad 4. El producto de dos funciones pares es una función par. Es decir: \[(f\cdot g)(-x)=(f\cdot g)(x)\] Demostración. Sean \(f\) y \(g\) dos funciones pares, es decir: \[\begin{aligned}f(-x)&=f(x)\\g(-x)&=g(x)\end{aligned}\] De acuerdo con el álgebra de funciones sabemos que: \[(f\cdot g)(x)=f(x)\cdot g(x)\] De tal manera que: \[\begin{aligned}(f\cdot g)(-x)&=f(-x)\cdot g(-x)\\&=f(x)\cdot g(x)\\&=(f\cdot g)(x)\end{aligned}\]
El producto de dos funciones impares es impar
Propiedad 5. El producto de dos funciones impares es una función par. Es decir: \[\begin{aligned}(f\cdot g)(-x)=(f\cdot g)(x)\end{aligned}\] Demostración. Sean \(f\) y \(g\) dos funciones impares, es decir: \[\begin{aligned}f(-x)&=-f(x)\\g(-x)&=-g(x)\end{aligned}\] Entonces:\[\begin{aligned}(f\cdot g)(-x)&=f(-x)\cdot g(-x)\\&=(-f(x))\cdot(-g(x))\\&=f(x)\cdot g(x)\\&=(f\cdot g)(x)\end{aligned}\]
El producto de una función par con una función impar es impar
Propiedad 6. El producto de una función par con una función impar es una función impar. Es decir: \[(f\cdot g)(-x)=-(f\cdot g)(x)\] Demostración. Sea \(f\) una función par y \(g\) una función impar, es decir: \[\begin{aligned}f(-x)&=f(x)\\g(-x)&=-g(x)\end{aligned}\] Entonces:\[\begin{aligned}(f\cdot g)(-x)&=f(-x)\cdot g(-x)\\&=f(x)\cdot -g(x)\\&=-(f(x)\cdot g(x))\\&=-(f\cdot g)(x)\end{aligned}\]
La composición de dos funciones pares es par
Propiedad 7. La composición de dos funciones pares es una función par. Es decir: \[(g\circ f)(x)=(g\circ f)(x)\] Demostración. Sean \(f\) y \(g\) dos funciones pares, es decir: \[\begin{aligned}f(-x)&=f(x)\\g(-x)&=g(x)\end{aligned}\] De acuerdo con la composición de funciones, la función compuesta de \(f\) con \(g\) se define por: \((g\circ f)(x)=g(f(x))\). Entonces:\[\begin{aligned}(g\circ f)(-x)&=g(f(-x))\\&=g(f(x))\\&=(g\circ f)(x)\end{aligned}\]
La composición de dos funciones impares es impar
Propiedad 8. La composición de dos funciones impares es una función impar. Es decir: \[(g\circ f)(x)=-(g\circ f)(x)\] Demostración.Sean \(f\) y \(g\) dos funciones impares, es decir:\[\begin{aligned}f(-x)&=-f(x)\\g(-x)&=-g(x)\end{aligned}\] Entonces: \[\begin{aligned}(g\circ f)(-x)&=g(f(-x))\\&=g(-f(x))\\&=-g(f(x))\\&=-(g\circ f)(x)\end{aligned}\]
Función definida en los números reales
Propiedad 9. Toda función definida en los números reales \(f:\mathbb{R}\rightarrow\mathbb{R}\) puede escribirse como la suma de una función par y una función impar. Es decir: \[f(x)=P(x)+I(x)\] Demostración. Sea \(P(x)\) una función par definida como:\[P(x)=\frac{f(x)-f(-x)}{2}\] Sea \(I(x)\) una función impar definida como: \[I(x)=\frac{f(x)+f(-x)}{2}\] Sumando estas funciones obtenemos que:
Paridad de las funciones trigonométricas
¿La función seno es par o impar?
La función seno es impar. Demostración: Una función \(f\) es impar si para cada valor de \(x\) en el dominio de \(f\): \[f(-x)=-f(x)\] Por lo tanto, la función seno es impar si se cumple que: \[\sin{-x}=-\sin{x}\] Para demostrar esto, consideremos la siguiente definición de la función seno: \[\sin(x)=\frac{e^{ix}-e^{-ix}}{2i}\] Ahora, calculemos \(-x\) en esta función: \[\begin{aligned}\sin{-x}&=\frac{e^{i(-x)}-e^{-i(-x)}}{2i}\\&=\frac{e^{-ix}-e^{ix}}{2i}\end{aligned}\] Observa que podemos multiplicar el numerador y el denominador por -1 sin alterar el valor de la expresión, es decir: \[\begin{aligned}\sin{-x}&=\frac{e^{-ix}-e^{ix}}{2i}\\&=\frac{-1}{-1}\frac{e^{-ix}-e^{ix}}{2i}\\&=\frac{-e^{-ix}+e^{ix}}{-2i}\\&=\frac{e^{ix}-e^{-ix}}{-2i}\\&=-\frac{e^{ix}-e^{-ix}}{2i}\end{aligned}\] Observa que esta última igualdad es igual a \(-\sin{x}\), es decir: \[\begin{aligned}\sin{-x}&=-\frac{e^{ix}-e^{-ix}}{2i}\\&=-\sin{x}\end{aligned}\] Por lo tanto, hemos demostrado que \(\sin{-x}=-\sin{x}\), lo que confirma que la función seno es una función impar.
¿La función coseno es par o impar?
La función coseno es par. Demostración: Una función \(f\) es par si para cada valor de \(x\) en el dominio de \(f\): \[f(-x)=f(x)\] Por lo tanto, la función coseno es una función par si se cumple que: \[\cos{-x} =\cos{x}\] Para demostrar esto, consideremos la definición de la función coseno: \[\cos{x}=\frac{e^{ix}+e^{-ix}}{2}\] Ahora, evaluemos \(-x\) en esta función: \[\begin{aligned}\cos{-x}&=\frac{e^{i(-x)}+e^{-i(-x)}}{2}\\&=\frac{e^{-ix}+e^{ix}}{2}\end{aligned}\] Observa que el numerador en \(\cos(-x)\) es idéntico al numerador en \(\cos(x)\), solo que los términos están en el orden inverso. Sin embargo, debido a que la suma es conmutativa, esto no afecta el resultado. Por lo tanto, podemos escribir: \[\cos{-x}=\frac{e^{ix}+e^{-ix}}{2}\] Y esto es igual a \(\cos(x)\), es decir: \[\begin{aligned}\cos{-x}&=\frac{e^{ix}+e^{-ix}}{2}\\&=\cos{x}\end{aligned}\] Por lo tanto, hemos demostrado que \(\cos{-x}=\cos{x}\), lo que confirma que la función coseno es una función par.
¿La función tangente es par o impar?
La función tangente es impar. Demostración: Una función \(f\) es impar si para cada valor de \(x\) en su dominio, se cumple que: \[f(-x)=-f(x)\] Por lo tanto, la función tangente será impar si cumple que: \[\tan{-x}=-\tan{x}\] Para demostrar esto, sea la función tangente definida como: \[\tan{x}=\frac{\sin{x}}{\cos{x}}\] Ahora, si evaluamos \(-x\) en la función obtenemos: \[\tan{-x}=\frac{\sin{-x}}{\cos{-x}}\] Como la función seno es una función impar: \[\sin{-x}=-\sin{x}\] y la función coseno es una función par: \[\cos{-x}=\cos{x}\] Obtenemos que: \[\begin{aligned}\tan{-x}&=\frac{\sin{-x}}{\cos{-x}}\\&=\frac{-\sin{x}}{\cos{x}}\\&=-\frac{\sin{x}}{\cos{x}}\\&=-\tan{x}\end{aligned}\] Esto demuestra que la función tangente es impar, ya que se cumple que: \[\tan{-x}=-\tan{x}\] para todos los valores de \(x\).
Función par y función impar ejercicios para practicar.
Ejercicio 1. Analice si la siguiente función es par, impar o ninguna de las dos. \[f(x)=x^2\] Ejercicio 2. Determine la paridad de la función \(g\) definida como: \[g(x)=\cos{3x}\] Ejercicio 3. Establezca la paridad de la siguiente función: \[h(x) = \sin{2x}\] Ejercicio 4. Investigue si la función \(k(x\) es una función par, impar o ninguna de las dos. \[k(x)=2x^3-2x\] Ejercicio 5. Determine la naturaleza de la siguiente función en términos de paridad: \[m(x)=e^x+e^{-x}\] Ejercicio 6. Identifique la paridad de la función \[p(x)=x^4-x^2\] Ejercicio 7. Analice si la siguiente función \(q(x)\) es una función par, impar o ni par ni impar. \[q(x)=\sin{x}+\cos{x}\] Ejercicio 8. Descubra si la función \(r(x)\) es una función par, impar o ninguna de las dos. \[r(x)=3x+\frac{1}{x}\] Ejercicio 9. Investigue si la siguiente función es una función par o impar, y proporcione una justificación. \[t(x) = x^2 + 1\] Ejercicio 10. Determine la paridad de \(s(x) = \sqrt{x^2}\) y explique su razonamiento.
Aplicaciones de las funciones pares e impares
Aplicación de una función par: Modelado de Espejos Cóncavos. En óptica, los espejos cóncavos son componentes utilizados en telescopios, faros de automóviles y otros dispositivos ópticos. Estos espejos son ejemplos de sistemas que pueden modelarse utilizando funciones pares. La razón es que los espejos cóncavos tienen una simetría central: cualquier rayo de luz que incide en el espejo a través de su eje principal se refleja a lo largo de una línea que pasa por el centro del espejo. La forma de la superficie del espejo, que es simétrica con respecto a su eje principal, se puede describir mediante una función par, como la ecuación de un espejo cóncavo.
Aplicación de una función impar: Estabilidad de un Péndulo Simple. El péndulo simple es un sistema mecánico comúnmente utilizado para ilustrar conceptos de física y matemáticas. Cuando se estudia la estabilidad de un péndulo simple, se utiliza el concepto de función impar. Si consideramos un péndulo simple en equilibrio, cualquier pequeña desviación angular (θ) de la posición vertical genera una fuerza restauradora proporcional a -θ, lo que significa que el sistema es descrito por una función impar. Esta propiedad de ser una función impar es fundamental para analizar la estabilidad del péndulo, ya que muestra que el sistema tiende a regresar a su posición de equilibrio cuando se desplaza.
Aplicación de una función par: Análisis de Señales de Audio. En el procesamiento de señales de audio, las funciones pares son útiles para representar componentes de señales de audio que son simétricos. Por ejemplo, cuando escuchamos música, muchas de las ondas sonoras en la música, como las notas musicales puras, pueden ser representadas por funciones pares, ya que son simétricas con respecto al tiempo. La representación en el dominio de la frecuencia de una señal de audio a menudo implica el uso de funciones pares, como la Transformada de Fourier, que descompone la señal en componentes armónicos simétricos.