Álgebra de funciones

El álgebra de funciones permite manipular y transformar funciones para obtener como resultado nuevas funciones que pueden ser más útiles o fáciles de analizar. Por ejemplo, dadas dos funciones \(f\) y \(g\), el álgebra de funciones permite sumarlas, restarlas, multiplicarlas, dividirlas y aplicarles otras operaciones para obtener como resultado una nueva función \(h\) que combina las propiedades de las funciones originales.

En esta entrada de blog, te mostraremos en que consiste el álgebra de funciones, qué conceptos básicos debes conocer, y cómo puedes aplicarlos para resolver problemas prácticos en diversas áreas, como la física, la ingeniería, la economía y más.

Álgebra de funciones

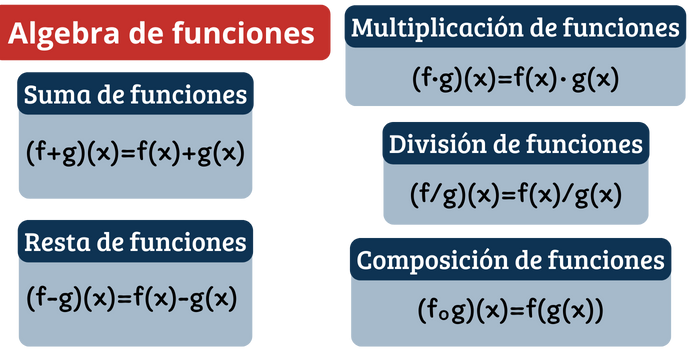
Igualdad de funciones

Dos funciones son consideradas iguales si comparten el mismo dominio y la misma regla de correspondencia. En otras palabras, dos funciones \(f(x)\) y \(g(x)\) son iguales si, para cualquier valor de \(x\) en su dominio, \(f(x)\) produce el mismo valor que \(g(x)\).

Es crucial tener en cuenta que, incluso cuando dos funciones tienen expresiones algebraicas diferentes, pueden ser consideradas iguales si generan los mismos resultados para todos los valores de \(x\) en su dominio.

¿Cómo determinar si dos funciones son iguales?

  • Paso 1. Calcular el dominio de cada una de las funciones.
  • Paso 2. Verificar que los dominios calculados sean idénticos. Si los dominios difieren, se puede concluir, desde este punto, que las funciones dadas no son iguales.
  • Paso 3. Confirmar que las reglas de correspondencia de las funciones sean las mismas. En este paso, puede ser necesario aplicar algún procedimiento algebraico para obtener la regla de correspondencia de una función a partir de la regla de correspondencia de la otra. Si las reglas de correspondencia no coinciden, entonces las funciones no son iguales.

Suma de funciones

Dadas dos funciones \(f(x)\) y \(g(x)\), la suma de funciones, representada como \(f+g\), se define como:

\[(f+g)(x)=f(x)+g(x)\]

Dominio de la función suma

El dominio de la función suma se determina mediante la siguiente expresión:

\[Dom_{(f+g)}=Dom_{f}\cap Dom_{g}\]

Si la intersección de los dominios es nula, entonces la función suma no está definida. Es decir, si \[Dom_{(f+g)}=\emptyset\] entonces no es posible definir \((f+g)(x)\)

¿Cómo hallar la suma de funciones?

  • Paso 1. Determinar el dominio de cada una de las funciones.
  • Paso 2. Encontrar la intersección de los dominios obtenidos. Si la intersección es vacía, se concluye que no es posible definir la suma de las funciones involucradas.
  • Paso 3. Definir la función suma de acuerdo a la definición.

Resta de funciones

Dadas dos funciones \(f(x)\) y \(g(x)\), la diferencia de funciones, denotada por \(f-g\), se define como:

\[(f-g)(x)=f(x)-g(x)\]

Dominio de la función diferencia

El dominio de la función diferencia se determina mediante la siguiente expresión:

\[Dom_{(f-g)}=Dom_{f}\cap Dom_{g}\]

Si la intersección de los dominios es nula, entonces la función diferencia no está definida. Es decir, si \[Dom_{(f-g)}=\emptyset\] entonces no es posible definir \((f-g)(x)\)

¿Cómo hallar la resta de funciones?

  • Paso 1. Determinar el dominio de cada una de las funciones.
  • Paso 2. Encontrar la intersección de los dominios obtenidos. Si la intersección es vacía, se concluye que la resta de las funciones involucradas no está definida.
  • Paso 3. Definir la función diferencia de acuerdo a la definición.

Multiplicación de funciones

Dadas dos funciones \(f(x)\) y \(g(x)\), el producto de funciones, denotado por \(f\cdot g\), se define como:

\[(f \cdot g)(x) = f(x) \cdot g(x)\]

Dominio de la función producto

El dominio de la función producto se determina mediante la siguiente expresión:

\[Dom_{(f\cdot g)}=Dom_{f}\cap Dom_{g}\]

Si la intersección de los dominios es nula, entonces la función producto no está definida. Es decir, si \[Dom_{(f\cdot g)}=\emptyset\] entonces no es posible definir \((f\cdot g)(x)\)

¿Cómo hallar el producto de funciones?

  • Paso 1. Determinar el dominio de cada función involucrada.
  • Paso 2. Encontrar la intersección de los dominios obtenidos. Si la intersección es igual al vacío, se concluye que el producto de las funciones involucradas no está definido.
  • Paso 3. Definir la función producto de acuerdo con la definición.

División de funciones

Dadas dos funciones \(f(x)\) y \(g(x)\), si \(g(x)\) no es igual a la función nula, el cociente de funciones, denotado por \(f/g\), se define como:

\[\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}\]

Dominio de la función cociente

El dominio de la función cociente se determina a partir de la siguiente expresión:

\[Dom_{(f/g)}=\left(Dom_{f}\cap Dom_{g}\right)-\left\lbrace x | g(x)=0\right\rbrace\]

Si la intersección de los dominios, excluyendo los valores de \(x\) para los cuales \(g(x) = 0\), es igual al vacío, entonces la función cociente no está definida. Es decir, si \[Dom_{(f/g)}=\emptyset\] entonces no es posible definir \((f/g)(x)\).

¿Cómo hallar el cociente de funciones?

  • Paso 1. Determinar el dominio de las funciones involucradas.
  • Paso 2. Encontrar los valores de \(x\) para los cuales \(g(x)=0\), es decir, los valores de \(x\) en los que la función que representa al divisor es cero.
  • Paso 3. Encontrar la intersección de los dominios obtenidos, y quitar los valores de \(x\) para los cuales la función que representa al divisor es cero. Si el conjunto resultante es igual al vacío, entonces el cociente de las funciones no está definido.
  • Paso 4. Definir la función cociente de acuerdo con la definición.

Composición de funciones

Dadas dos funciones, \(f(x)\) y \(g(x)\), se define la composición de funciones, de \(f\) compuesta con \(g\), denotado por \((g\circ f)\), como:

\[(g\circ f)(x)=g(f(x))\]

De manera similar, se define la composición de funciones, de \(g\) compuesta con \(f\), denotado por \((f\circ g)(x)\), como:

\[(f\circ g)(x)=f(g(x))\]

Es importante tener en cuenta que el orden de la composición es importante y que, en general, la composición de funciones no es conmutativa, lo que significa que \((g\circ f)\) y \((f\circ g)\) pueden dar resultados diferentes y solo en algunos casos especiales estas composiciones podrían ser iguales.

Dominio de la composición de funciones

El dominio de la composición, de \(f\) compuesta con \(g\), consta de todos los valores de \(x\) del dominio de la función \(f\) para las cuales \(f(x)\) está en el dominio de \(g\). Es decir:

\[Dom_{(g \circ f)}=\left\lbrace x|x\in Dom_{f} \wedge f(x)\in Dom_{g}\right\rbrace\]

Al mencionar \(f(x)\) nos referimos al rango de \(f\), es decir, para poder definir la composición se debe asegurar que el rango de la función \(f\) sea un subconjunto del dominio de \(g\).

El dominio de la composición, de \(g\) compuesta con \(f\), consta de todos los valores de \(x\) del dominio de la función \(g\) para los cuales \(g(x)\) está en el dominio de \(f\). Es decir:

\[Dom_{(f \circ g)}=\left\lbrace x|x\in Dom_{g} \wedge g(x)\in Dom_{f}\right\rbrace\]

Nuevamente, al mencionar \(g(x)\) nos referimos al rango de \(g(x)\), es decir, para poder definir la composición se debe asegurar que el rango de la función \(g\) sea un subconjunto del dominio de \(f\).

Algebra de funciones ejercicios para practicar

Ejercicio 1. Dadas las funciones \(f(x)=2x+3\) y \(g(x)=x^2\), encuentra la función suma \(f+g\).

Ejercicio 2. Dadas las funciones \(h(x)=4x-1\) y \(k(x)=2x^2\), calcula la función diferencia \(h-k\).

Ejercicio 3: Si \(p(x)=3x\) y \(q(x)=x^2+1\), determina el producto de funciones \(p\cdot q\).

Ejercicio 4. Dadas las funciones \(u(x)=5x\) y \(v(x)=x^2-3\), encuentra el cociente de funciones \(u/v\) (asegúrate de verificar el dominio).

Ejercicio 5. Dadas las funciones \(m(x)=x+2\) y \(n(x)=3x^2\), determina la suma de funciones \(m+n\).

Ejercicio 6. Si \(s(x)=4x\) y \(t(x)=x^2-2\), calcula la resta de funciones \(s-t\).

Ejercicio 7. Encuentra el producto de las funciones \(w(x)=2x\) y \(z(x)=x^2+1\).

Ejercicio 8. Dadas las funciones \(a(x)=3x+1\) y \(b(x)=x^2-5\), encuentra la función cociente \(a/b\) (verifica el dominio).